De algoritmische wereld is prachtig, met veelsoortige strategieën en hulpmiddelen die 24 uur per dag worden ontwikkeld om tegemoet te komen aan de behoefte aan high-performance computing. Wanneer algoritmen worden geïnspireerd door natuurwetten, worden er zelfs interessante resultaten waargenomen. Evolutionaire algoritmen behoren tot een dergelijke klasse van algoritmen. Deze algoritmen zijn ontworpen om bepaald gedrag en evolutionaire kenmerken van het menselijk genoom na te bootsen. Bovendien is dergelijk algoritmisch ontwerp niet alleen beperkt tot mensen, maar kan het ook worden geïnspireerd door het natuurlijke gedrag van bepaalde dieren. Het fundamentele doel van het vervaardigen van dergelijke methodologieën is het bieden van realistische, relevante en toch goedkope oplossingen voor problemen die tot nu toe onoplosbaar waren met conventionele middelen.

Verschillende optimalisatietechnieken zijn dus geëvolueerd op basis van dergelijke evolutionaire algoritmen en hebben daarmee het domein van de metaheuristiek geopend. Metaheuristisch is afgeleid van twee Griekse woorden, namelijk: Meta betekenis één niveau hoger En heuriskein betekenis vinden . Algoritmen zoals de Particle Swarm Optimization (PSO) en Ant Colony Optimization (ACO) zijn voorbeelden van zwermintelligentie en metaheuristieken. Het doel van zwermintelligentie is het ontwerpen van intelligente multi-agentsystemen door inspiratie te halen uit het collectieve gedrag van sociale insecten zoals mieren, termieten, bijen, wespen en andere dierengemeenschappen zoals zwermen vogels of scholen vissen.

Achtergrond:

Ant Colony Optimization-techniek is puur geïnspireerd op de foerageren gedrag van mierenkolonies, voor het eerst geïntroduceerd door Marco Dorigo in de jaren negentig. Mieren zijn eusociale insecten die de voorkeur geven aan overleving en instandhouding van een gemeenschap in plaats van als individuele soort. Ze communiceren met elkaar via geluid, aanraking en feromoon. Feromonen zijn organische chemische verbindingen die worden afgescheiden door de mieren en die een sociale reactie uitlokken bij leden van dezelfde soort. Dit zijn chemicaliën die in staat zijn zich als hormonen te gedragen buiten het lichaam van het afscheidende individu, en zo het gedrag van het ontvangende individu te beïnvloeden. Omdat de meeste mieren op de grond leven, gebruiken ze het bodemoppervlak om feromoonsporen achter te laten die door andere mieren kunnen worden gevolgd (geroken).
Mieren leven in gemeenschapsnesten en het onderliggende principe van ACO is het observeren van de beweging van de mieren vanuit hun nest om zo via de kortst mogelijke weg naar voedsel te zoeken. Aanvankelijk beginnen mieren willekeurig rond hun nesten te bewegen op zoek naar voedsel. Deze gerandomiseerde zoektocht opent meerdere routes van het nest naar de voedselbron. Nu dragen mieren, afhankelijk van de kwaliteit en kwantiteit van het voedsel, een deel van het voedsel terug met de nodige feromoonconcentratie op de terugweg. Afhankelijk van deze feromoonproeven zou de waarschijnlijkheid van selectie van een specifiek pad door de volgende mieren een leidende factor zijn voor de voedselbron. Blijkbaar is deze waarschijnlijkheid gebaseerd op zowel de concentratie als de verdampingssnelheid van feromoon. Er kan ook worden opgemerkt dat, aangezien de verdampingssnelheid van feromoon ook een beslissende factor is, de lengte van elk pad gemakkelijk in rekening kan worden gebracht.

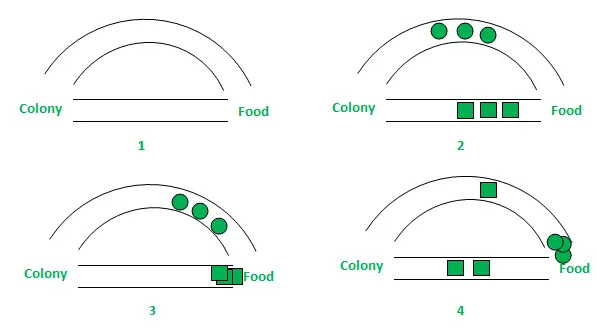
In de bovenstaande figuur zijn eenvoudigheidshalve slechts twee mogelijke routes tussen de voedselbron en het mierennest in beschouwing genomen. De fasen kunnen als volgt worden geanalyseerd:

Fase 1: Alle mieren zitten in hun nest. Er is geen feromoongehalte in de omgeving. (Voor algoritmisch ontwerp kan rekening worden gehouden met de hoeveelheid restferomoon zonder de waarschijnlijkheid te verstoren) Fase 2: Mieren beginnen hun zoektocht met een gelijke (elk 0,5) waarschijnlijkheid langs elk pad. Het is duidelijk dat het gebogen pad het langste is en dat de tijd die mieren nodig hebben om de voedselbron te bereiken groter is dan het andere. Fase 3: De mieren bereiken via het kortere pad eerder de voedselbron. Nu worden ze kennelijk geconfronteerd met een soortgelijk selectiedilemma, maar deze keer is de kans op selectie groter vanwege het feromoonspoor langs het kortere pad dat al beschikbaar is. Fase 4: Via het kortere pad keren meer mieren terug en vervolgens nemen ook de feromoonconcentraties toe. Bovendien neemt als gevolg van verdamping de feromoonconcentratie in het langere pad af, waardoor de kans kleiner wordt dat dit pad in verdere fasen wordt geselecteerd. Daarom gebruikt de hele kolonie geleidelijk het kortere pad bij hogere waarschijnlijkheden. Padoptimalisatie wordt dus bereikt.

Algoritmisch ontwerp:

Met betrekking tot het bovenstaande gedrag van de mieren kan nu een algoritmisch ontwerp worden ontwikkeld. Voor de eenvoud is er rekening gehouden met één enkele voedselbron en één mierenkolonie met slechts twee mogelijke routes. Het hele scenario kan worden gerealiseerd door middel van gewogen grafieken waarin de mierenkolonie en de voedselbron fungeren als hoekpunten (of knooppunten); de paden dienen als randen en de feromoonwaarden zijn de gewichten die bij de randen horen.
Laat de grafiek dat zijn G = (V, E) waarbij V, E de randen en de hoekpunten van de grafiek zijn. De hoekpunten volgens onze overweging zijn IN_S (Bron hoekpunt – mierenkolonie) en IN_D (Bestemmingshoekpunt – Voedselbron), De twee randen zijn dat wel EN₁ En EN₂ met lengtes L₁ En L₂ aan elk toegewezen. Nu kan worden aangenomen dat de bijbehorende feromoonwaarden (die een indicatie zijn voor hun sterkte) dat wel zijn R₁ En R₂ voor hoekpunten E₁en E₂respectievelijk. Dus voor elke mier is de startwaarschijnlijkheid van padkeuze (tussen E₁en E₂) kan als volgt worden uitgedrukt:

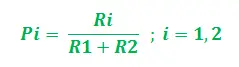
Het is duidelijk dat als R₁>R₂, de waarschijnlijkheid om E te kiezen₁hoger is en omgekeerd. Zeg nu, terwijl je via dit kortste pad terugkeert, E_i, wordt de feromoonwaarde bijgewerkt voor het overeenkomstige pad. De update wordt gedaan op basis van de lengte van de paden en de verdampingssnelheid van feromoon. De update kan dus stapsgewijs als volgt worden gerealiseerd:

Afhankelijk van de padlengte –

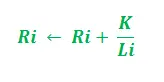
In de bovenstaande update is i = 1, 2 en dient ‘K’ als parameter van het model. Bovendien is de update afhankelijk van de lengte van het pad. Hoe korter het pad, hoe hoger het toegevoegde feromoon. In overeenstemming met de verdampingssnelheid van feromoon –

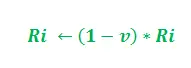
De parameter ‘v’ behoort tot interval (0, 1] dat de feromoonverdamping regelt. Verder is i = 1, 2.

Bij elke iteratie worden alle mieren op bronpunt V geplaatst_S(mierenkolonie). Vervolgens verplaatsen mieren zich van V_Saan V_D(voedselbron) na stap 1. Vervolgens voeren alle mieren hun terugreis uit en versterken ze hun gekozen pad op basis van stap 2.

Pseudocode:

 Procedure AntColonyOptimization: Initialize necessary parameters and pheromone trials; while not termination do : Generate ant population; Calculate fitness values associated with each ant; Find best solution through selection methods; Update pheromone trial; end while end procedure>

De feromoonupdate en de fitnessberekeningen in de bovenstaande pseudocode kunnen worden gevonden via de hierboven genoemde stapsgewijze implementaties.
Zo is de introductie van de ACO-optimalisatietechniek tot stand gekomen. De toepassing van de ACO kan worden uitgebreid tot verschillende problemen, zoals de beroemde TSP (handelsreizigerprobleem) .

Referenties:
https://www.ics.uci.edu/~welling/teaching/271fall09/antcolonyopt.pdf