Driehoeken zijn driezijdige gesloten veelhoeken gevormd door het snijpunt van drie lijnen. In het dagelijks leven kom je het veel tegen. Het is een van de basisvormen van de geometrie. Het heeft drie zijden, drie hoeken en drie hoekpunten. Een rechthoekige driehoek is een driehoek waarbij een van de hoeken altijd gelijk is aan 90°. De stelling van Pythagoras is afgeleid voor rechthoekige driehoeken, waarin staat dat het kwadraat van de hypotenusa (de langste zijde) gelijk is aan de som van de kwadraten van basis en loodlijn.

Gegeven de lengte van ten minste twee zijden van een rechthoekige driehoek, kunnen we de waarde van elke hoek van de rechthoekige driehoek vinden. Hiervoor gebruiken we verschillende trigonometrische functies zoals sinus, cosinus, tangens, cotangens, sec en cosec. Deze helpen ons de hoeken van een rechthoekige driehoek in verband te brengen met de zijden.

Eigenschappen

• Er is een rechthoekig hoekpunt tussen de drie hoekpunten
• De zijde tegenover het rechthoekige hoekpunt wordt de hypotenusa .
• De lengte van de zijden volgt de stelling van Pythagoras, die stelt

hypotenusa ² = basis ² + hoogte ²

• De hypotenusa is de langste zijde van een rechthoekige driehoek.
• De andere hoeken dan de rechte hoek zijn scherpe hoeken, aangezien de waarde kleiner is dan 90^O

Trigonometrische functies

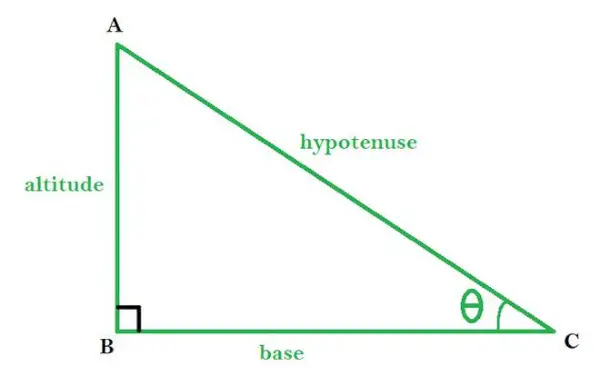
ABC is een rechthoekige driehoek met ∠B als rechthoekige hoek

probeer Java te vangen

• cosθ: Dit geeft de verhouding van de basis tot de hypotenusa van een rechthoekige driehoek.

cosθ = basis / hypotenusa

• zondeθ: Dit geeft de verhouding van de hoogte door de hypotenusa van een rechthoekige driehoek.

sinθ = hoogte / hypotenusa

• tanθ: Het is de verhouding tussen de hoogte en de basis van een rechthoekige driehoek.

tanθ = hoogte / basis

• kinderbedθ: Het is het omgekeerde van tanθ
• secθ: Het is het omgekeerde van cosθ
• cosecθ: Het is het omgekeerde van sinθ

Om de hoeken van een rechthoekige driehoek te vinden, kunnen we de trigonometrische inverse nemen van de verhouding van gegeven zijden van de driehoek.

Voorbeeld:

Als sinθ = x, dan kunnen we schrijven

θ = zonde ^-1 X.

Dit retourneert de hoek waarvoor de sinuswaarde van de hoek x is.

Op dezelfde manier bestaat er cos^-1θ, dus^-1ik, kinderbed^-1θ, sec^-1θ, en cosec^-1i

Voorbeeldproblemen

Vraag 1. Gegeven een rechthoekige driehoek, waarbij de basis gelijk is aan 10 cm en de hypotenusa gelijk is aan 20 cm. Zoek de waarde van de basishoek.

Oplossing:

Gegeven, basis = 10 cm

Hypotenusa = 20cm

Stel dat de waarde van de basishoek θ is. We kunnen schrijven

cosθ = basis / hypotenusa = 10/20 = 1/2

θ = cos^-1(1/2) = 60^O

De waarde van de basishoek is dus 60 ^O .

Vraag 2. Bereken de waarde van de hoeken van een rechthoekige driehoek, gegeven dat een van de scherpe hoeken tweemaal de andere is.

Oplossing:

Omdat we weten dat de som van alle drie de hoeken in een driehoek 180 is^O.

Omdat een van de hoeken 90 is^Oen een van de scherpe hoeken is tweemaal de andere, we kunnen ze beschouwen als θ en 2θ.

Wij kunnen dus schrijven

90^O+ θ + 2 θ = 180^O

3θ = 180^O– 90^O

3θ = 90^O

θ = 90^O/3 = 30 ^O

2θ = 2 × 30^O= 60 ^O

De hoeken zijn dus 30 ^O , 60 ^O , en 90 ^O .

Vraag 3. Bereken de waarde van de elevatiehoek van een ladder met een lengte van 5 meter, gegeven dat de basis van de ladder zich op een afstand van 3 meter van de muur bevindt.

Oplossing:

Omdat de ladder fungeert als hypotenusa van een rechthoekige driehoek en de basisafstand gelijk is aan 3 meter, kunnen we schrijven

Hypotenusa = 5m

Basis = 3m

Laat de elevatiehoek θ zijn. Wij kunnen dus schrijven

cosθ = Basis / Hypotenusa = 3/5

θ = cos^-1(3/5)

θ = 53^O

De waarde van de elevatiehoek is dus 53^O.

Vraag 4. Vind de waarde van de hypotenusa, gegeven dat de lengte van de hoogte 8 m is en de basishoek gelijk is aan 30 ^O .

Oplossing:

Gegeven is dat de basishoek gelijk is aan 30^Oen de hoogte gelijk is aan 8 meter, kunnen we de sinusfunctie toepassen om de lengte van de hypotenusa te vinden.

zonde30 ^O = hoogte / hypotenusa

hypotenusa = hoogte / sin30^O

Sinds de waarde van sin30^Ogelijk is aan 1/2, kunnen we schrijven

hypotenusa = hoogte / (1/2) = 2 × hoogte

Dus hypotenusa = 2 × 8 = 16m

De lengte van de hypotenusa is dus gelijk aan 16 meter.