Euleriaans pad is een pad in een grafiek dat elke rand precies één keer bezoekt. Euleriaans circuit is een Euleriaans pad dat op hetzelfde hoekpunt begint en eindigt.
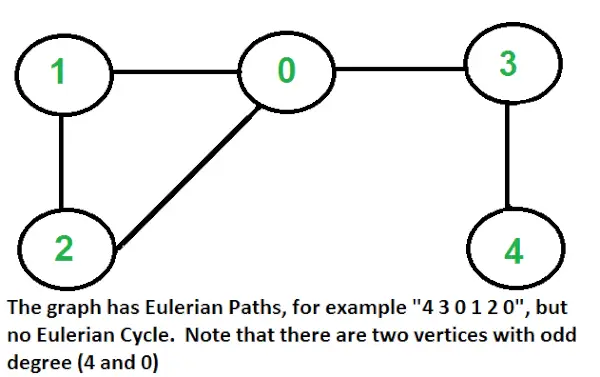


Hoe kom je erachter of een bepaalde grafiek Euleriaans is of niet?
Het probleem is hetzelfde als de volgende vraag. Is het mogelijk om een bepaalde grafiek te tekenen zonder het potlood van het papier te halen en zonder de randen meer dan één keer over te trekken?
Een graaf wordt Euleriaans genoemd als deze een Euleriaanse cyclus heeft, en Semi-Euleriaans als deze een Euleriaans pad heeft. Het probleem lijkt op het Hamiltoniaanse pad, wat een NP-volledig probleem is voor een algemene grafiek. Gelukkig kunnen we in polynomiale tijd ontdekken of een bepaalde grafiek een Euleriaans pad heeft of niet. In feite kunnen we het vinden in O(V+E) tijd.
Hieronder volgen enkele interessante eigenschappen van ongerichte grafieken met een Euleriaans pad en cyclus. We kunnen deze eigenschappen gebruiken om te bepalen of een grafiek Euleriaans is of niet.
Euleriaanse cyclus: Een ongerichte grafiek heeft een Euleriaanse cyclus als de volgende twee voorwaarden waar zijn.
- Alle hoekpunten met een andere graad dan nul zijn verbonden. We geven niets om hoekpunten met nul graden, omdat ze niet tot de Euleriaanse cyclus of het pad behoren (we houden alleen rekening met alle randen).
- Alle hoekpunten hebben een gelijke graad.
Euleriaans pad: Een ongerichte grafiek heeft een Euleriaans pad als de volgende twee voorwaarden waar zijn.
- Hetzelfde als voorwaarde (a) voor de Euleriaanse cyclus.
- Als nul of twee hoekpunten een oneven graad hebben en alle andere hoekpunten een even graad hebben. Merk op dat slechts één hoekpunt met een oneven graad niet mogelijk is in een ongerichte grafiek (de som van alle graden is altijd even in een ongerichte grafiek)
Merk op dat een grafiek zonder randen als Euleriaans wordt beschouwd omdat er geen randen zijn om doorheen te lopen.
Hoe werkt dit?
In het Euleriaanse pad lopen we elke keer dat we een hoekpunt v bezoeken, door twee niet bezochte randen met één eindpunt als v. Daarom moeten alle middelste hoekpunten in het Euleriaanse pad een gelijke graad hebben. Voor de Euleriaanse cyclus kan elk hoekpunt een middenhoekpunt zijn, daarom moeten alle hoekpunten een gelijke graad hebben.
Implementatie:
C++
knipprogramma in ubuntu
// A C++ program to check if a given graph is Eulerian or not> #include> #include> using> namespace> std;> // A class that represents an undirected graph> class> Graph> {> >int> V;>// No. of vertices> >list<>int>>*bijvoeglijk naamwoord;>// A dynamic array of adjacency lists> public>:> >// Constructor and destructor> >Graph(>int> V) {>this>->V = V; bijvoeglijk naamwoord =>new> list<>int>>[IN]; }> >~Graph() {>delete> [] adj; }>// To avoid memory leak> >// function to add an edge to graph> >void> addEdge(>int> v,>int> w);> >// Method to check if this graph is Eulerian or not> >int> isEulerian();> >// Method to check if all non-zero degree vertices are connected> >bool> isConnected();> >// Function to do DFS starting from v. Used in isConnected();> >void> DFSUtil(>int> v,>bool> visited[]);> };> void> Graph::addEdge(>int> v,>int> w)> {> >adj[v].push_back(w);> >adj[w].push_back(v);>// Note: the graph is undirected> }> void> Graph::DFSUtil(>int> v,>bool> visited[])> {> >// Mark the current node as visited and print it> >visited[v] =>true>;> >// Recur for all the vertices adjacent to this vertex> >list<>int>>::iterator i;> >for> (i = adj[v].begin(); i != adj[v].end(); ++i)> >if> (!visited[*i])> >DFSUtil(*i, visited);> }> // Method to check if all non-zero degree vertices are connected.> // It mainly does DFS traversal starting from> bool> Graph::isConnected()> {> >// Mark all the vertices as not visited> >bool> visited[V];> >int> i;> >for> (i = 0; i visited[i] = false; // Find a vertex with non-zero degree for (i = 0; i if (adj[i].size() != 0) break; // If there are no edges in the graph, return true if (i == V) return true; // Start DFS traversal from a vertex with non-zero degree DFSUtil(i, visited); // Check if all non-zero degree vertices are visited for (i = 0; i if (visited[i] == false && adj[i].size()>0) retourneert onwaar; retourneer waar; } /* De functie retourneert een van de volgende waarden 0 --> Als de grafiek niet Euleriaans is 1 --> Als de grafiek een Euler-pad heeft (Semi-Euleriaans) 2 --> Als de grafiek een Euler-circuit heeft (Euleriaans) */ int Graph::isEulerian() {// Controleer of alle hoekpunten die niet nul graden zijn, verbonden zijn als (isConnected() == false) 0 retourneert; // Tel hoekpunten met een oneven graad int oneven = 0; for (int i = 0; i if (adj[i].size() & 1) odd++; // Als het aantal meer dan 2 is, dan is de grafiek niet Euleriaans als (oneven> 2) 0 retourneert; // Indien oneven telling is 2, dan semi-euleriaans. // Als de oneven telling 0 is, dan is de oneven telling nooit 1 voor ongerichte grafiekretour (oneven) } // Functie om testgevallen uit te voeren test(Grafiek &g) { int res = g.isEulerian(); if (res == 0) cout<< 'graph is not Eulerian
'; else if (res == 1) cout << 'graph has a Euler path
'; else cout << 'graph has a Euler cycle
'; } // Driver program to test above function int main() { // Let us create and test graphs shown in above figures Graph g1(5); g1.addEdge(1, 0); g1.addEdge(0, 2); g1.addEdge(2, 1); g1.addEdge(0, 3); g1.addEdge(3, 4); test(g1); Graph g2(5); g2.addEdge(1, 0); g2.addEdge(0, 2); g2.addEdge(2, 1); g2.addEdge(0, 3); g2.addEdge(3, 4); g2.addEdge(4, 0); test(g2); Graph g3(5); g3.addEdge(1, 0); g3.addEdge(0, 2); g3.addEdge(2, 1); g3.addEdge(0, 3); g3.addEdge(3, 4); g3.addEdge(1, 3); test(g3); // Let us create a graph with 3 vertices // connected in the form of cycle Graph g4(3); g4.addEdge(0, 1); g4.addEdge(1, 2); g4.addEdge(2, 0); test(g4); // Let us create a graph with all vertices // with zero degree Graph g5(3); test(g5); return 0; }> |
>
>
Java
// A Java program to check if a given graph is Eulerian or not> import> java.io.*;> import> java.util.*;> import> java.util.LinkedList;> // This class represents an undirected graph using adjacency list> // representation> class> Graph> {> >private> int> V;>// No. of vertices> >// Array of lists for Adjacency List Representation> >private> LinkedList adj[];> >// Constructor> >Graph(>int> v)> >{> >V = v;> >adj =>new> LinkedList[v];> >for> (>int> i=>0>; i adj[i] = new LinkedList(); } //Function to add an edge into the graph void addEdge(int v, int w) { adj[v].add(w);// Add w to v's list. adj[w].add(v); //The graph is undirected } // A function used by DFS void DFSUtil(int v,boolean visited[]) { // Mark the current node as visited visited[v] = true; // Recur for all the vertices adjacent to this vertex Iterator i = adj[v].listIterator(); while (i.hasNext()) { int n = i.next(); if (!visited[n]) DFSUtil(n, visited); } } // Method to check if all non-zero degree vertices are // connected. It mainly does DFS traversal starting from boolean isConnected() { // Mark all the vertices as not visited boolean visited[] = new boolean[V]; int i; for (i = 0; i visited[i] = false; // Find a vertex with non-zero degree for (i = 0; i if (adj[i].size() != 0) break; // If there are no edges in the graph, return true if (i == V) return true; // Start DFS traversal from a vertex with non-zero degree DFSUtil(i, visited); // Check if all non-zero degree vertices are visited for (i = 0; i if (visited[i] == false && adj[i].size()>0) retourneert onwaar; retourneer waar; } /* De functie retourneert een van de volgende waarden 0 --> Als de grafiek niet Euleriaans is 1 --> Als de grafiek een Euler-pad heeft (Semi-Euleriaans) 2 --> Als de grafiek een Euler-circuit heeft (Euleriaans) */ int isEulerian() {// Controleer of alle hoekpunten die niet nul graden zijn, verbonden zijn als (isConnected() == false) 0 retourneert; // Tel hoekpunten met een oneven graad int oneven = 0; for (int i = 0; i if (adj[i].size()%2!=0) odd++; // Als het aantal meer dan 2 is, dan is de grafiek niet Euleriaans als (oneven> 2) 0 retourneert; / / Als de oneven telling 2 is, dan is de oneven telling 0, dan is eulerian // Merk op dat de oneven telling nooit 1 kan zijn voor ongerichte grafiekretouren (oneven==2)? Functie om testgevallen uit te voeren void test() { int res = isEulerian(); (res == 0) System.out.println('graph is not Eulerian'); out.println('grafiek heeft een Euler-pad'); else System.out.println('grafiek heeft een Euler-cyclus' } // Driver-methode public static void main(String args[]) { / / Laten we de grafieken uit bovenstaande figuren maken en testen. Grafiek g1 = new Graph(5); g1.addEdge(0, 2); (0, 3); g1.addEdge(3, 4); Grafiek g2 = nieuwe Grafiek(5); addEdge(2, 1); g2.addEdge(0, 3); g2.addEdge(3, 4); g2.test(5); .addEdge(1, 0); g3.addEdge(0, 2); g3.addEdge(2, 1); g3.addEdge(0, 3); g3.addEdge(3, 4); g3.addEdge(1, 3); g3.test(); // Laten we een grafiek maken met 3 hoekpunten // verbonden in de vorm van een cyclus Grafiek g4 = nieuwe Grafiek(3); g4.addEdge(0, 1); g4.addEdge(1, 2); g4.addEdge(2, 0); g4.test(); // Laten we een grafiek maken met alle hoekpunten // met nul graden Grafiek g5 = new Graph(3); g5.test(); } } // Deze code is bijgedragen door Aakash Hasija> |
>
>
Python3
tekenreeksarray
# Python program to check if a given graph is Eulerian or not> #Complexity : O(V+E)> from> collections>import> defaultdict> # This class represents a undirected graph using adjacency list representation> class> Graph:> >def> __init__(>self>, vertices):> >self>.V>=> vertices># No. of vertices> >self>.graph>=> defaultdict(>list>)># default dictionary to store graph> ># function to add an edge to graph> >def> addEdge(>self>, u, v):> >self>.graph[u].append(v)> >self>.graph[v].append(u)> ># A function used by isConnected> >def> DFSUtil(>self>, v, visited):> ># Mark the current node as visited> >visited[v]>=> True> ># Recur for all the vertices adjacent to this vertex> >for> i>in> self>.graph[v]:> >if> visited[i]>=>=> False>:> >self>.DFSUtil(i, visited)> >'''Method to check if all non-zero degree vertices are> >connected. It mainly does DFS traversal starting from> >node with non-zero degree'''> >def> isConnected(>self>):> ># Mark all the vertices as not visited> >visited>=> [>False>]>*>(>self>.V)> ># Find a vertex with non-zero degree> >for> i>in> range>(>self>.V):> >if> len>(>self>.graph[i]) !>=> 0>:> >break> ># If there are no edges in the graph, return true> >if> i>=>=> self>.V>->1>:> >return> True> ># Start DFS traversal from a vertex with non-zero degree> >self>.DFSUtil(i, visited)> ># Check if all non-zero degree vertices are visited> >for> i>in> range>(>self>.V):> >if> visited[i]>=>=> False> and> len>(>self>.graph[i])>>0>:> >return> False> >return> True> >'''The function returns one of the following values> >0 -->Als de grafiek niet Euleriaans is> >1 -->Als de grafiek een Euler-pad heeft (Semi-Euleriaans)> >2 -->Als de grafiek een Euler Circuit (Euleriaans) '''>'> heeft isEulerian(>self>):> ># Check if all non-zero degree vertices are connected> >if> self>.isConnected()>=>=> False>:> >return> 0> >else>:> ># Count vertices with odd degree> >odd>=> 0> >for> i>in> range>(>self>.V):> >if> len>(>self>.graph[i])>%> 2> !>=> 0>:> >odd>+>=> 1> >'''If odd count is 2, then semi-eulerian.> >If odd count is 0, then eulerian> >If count is more than 2, then graph is not Eulerian> >Note that odd count can never be 1 for undirected graph'''> >if> odd>=>=> 0>:> >return> 2> >elif> odd>=>=> 2>:> >return> 1> >elif> odd>>2>:> >return> 0> ># Function to run test cases> >def> test(>self>):> >res>=> self>.isEulerian()> >if> res>=>=> 0>:> >print>(>'graph is not Eulerian'>)> >elif> res>=>=> 1>:> >print>(>'graph has a Euler path'>)> >else>:> >print>(>'graph has a Euler cycle'>)> # Let us create and test graphs shown in above figures> g1>=> Graph(>5>)> g1.addEdge(>1>,>0>)> g1.addEdge(>0>,>2>)> g1.addEdge(>2>,>1>)> g1.addEdge(>0>,>3>)> g1.addEdge(>3>,>4>)> g1.test()> g2>=> Graph(>5>)> g2.addEdge(>1>,>0>)> g2.addEdge(>0>,>2>)> g2.addEdge(>2>,>1>)> g2.addEdge(>0>,>3>)> g2.addEdge(>3>,>4>)> g2.addEdge(>4>,>0>)> g2.test()> g3>=> Graph(>5>)> g3.addEdge(>1>,>0>)> g3.addEdge(>0>,>2>)> g3.addEdge(>2>,>1>)> g3.addEdge(>0>,>3>)> g3.addEdge(>3>,>4>)> g3.addEdge(>1>,>3>)> g3.test()> # Let us create a graph with 3 vertices> # connected in the form of cycle> g4>=> Graph(>3>)> g4.addEdge(>0>,>1>)> g4.addEdge(>1>,>2>)> g4.addEdge(>2>,>0>)> g4.test()> # Let us create a graph with all vertices> # with zero degree> g5>=> Graph(>3>)> g5.test()> # This code is contributed by Neelam Yadav> |
>
>
C#
// A C# program to check if a given graph is Eulerian or not> using> System;> using> System.Collections.Generic;> > // This class represents an undirected graph using adjacency list> // representation> public> class> Graph> {> >private> int> V;>// No. of vertices> > >// Array of lists for Adjacency List Representation> >private> List<>int>>[]bijvoeglijk naamwoord;> > >// Constructor> >Graph(>int> v)> >{> >V = v;> >adj =>new> List<>int>>[in];> >for> (>int> i=0; i adj[i] = new List |
>
>
als het anders bashen is
Javascript
> // A Javascript program to check if a given graph is Eulerian or not> // This class represents an undirected graph using adjacency list> // representation> class Graph> {> >// Constructor> >constructor(v)> >{> >this>.V = v;> >this>.adj =>new> Array(v);> >for> (let i = 0; i this.adj[i] = []; } // Function to add an edge into the graph addEdge(v,w) { this.adj[v].push(w);// Add w to v's list. this.adj[w].push(v); //The graph is undirected } // A function used by DFS DFSUtil(v,visited) { // Mark the current node as visited visited[v] = true; // Recur for all the vertices adjacent to this vertex for(let i of this.adj[v]) { let n = i; if (!visited[n]) this.DFSUtil(n, visited); } } // Method to check if all non-zero degree vertices are // connected. It mainly does DFS traversal starting from isConnected() { // Mark all the vertices as not visited let visited = new Array(this.V); let i; for (i = 0; i |
>
>Uitvoer
graph has a Euler path graph has a Euler cycle graph is not Eulerian graph has a Euler cycle graph has a Euler cycle>
Tijdcomplexiteit: O(V+E)
Ruimtecomplexiteit: O(V+E)
Volgende artikelen:
Euleriaans pad en circuit voor gerichte grafieken.
Fleury’s algoritme om een Euleriaans pad of circuit af te drukken?
