Convolutie wordt voor veel dingen gebruikt, zoals het berekenen van afgeleiden, het detecteren van randen, het toepassen van vervagingen etc. en dit alles wordt gedaan met behulp van een 'convolutiekernel'. Een convolutiekernel is een zeer kleine matrix en in deze matrix heeft elke cel een nummer en ook een ankerpunt.
Het ankerpunt wordt gebruikt om de positie van de kernel ten opzichte van de afbeelding te kennen. Het begint in de linkerbovenhoek van de afbeelding en beweegt opeenvolgend over elke pixel. Kernel overlapt enkele pixels op elke positie in de afbeelding. Elke pixel die overlapt, wordt vermenigvuldigd en vervolgens toegevoegd. En de som wordt ingesteld als de waarde van de huidige positie.
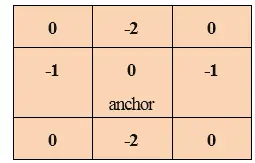
Convolutie is het proces waarbij elk element van de afbeelding wordt toegevoegd aan zijn lokale buren, en vervolgens wordt gewogen door de kernel. Het is gerelateerd aan een vorm van wiskundige convolutie.
In Convolutie voert de matrix geen traditionele matrixvermenigvuldiging uit, maar wordt deze aangegeven met *.
Stel dat er twee 3x3-matrices zijn, de ene is een kernel en de andere is een afbeeldingsstuk. Bij convolutie worden rijen en kolommen van de kernel omgedraaid en vervolgens vermenigvuldigd en vervolgens opgeteld. Elementen die aanwezig zijn in het midden van de matrix, d.w.z. in [2,2] van het beeld, zullen een gewogen combinatie van de beeldmatrix zijn en de gewichten zullen worden gegeven door de kernel. Op dezelfde manier worden alle andere elementen van de matrix gewogen en vervolgens worden de gewichten berekend.
Hieronder volgt pseudocode om het convolutieproces te beschrijven:
turbo c++ downloaden
For each image row in input image: For each pixel in image row: Set accumulator to zero For each kernel row in kernel: For each element in kernel row: If element position corresponding* to pixel position then Multiply element value corresponding*to pixelvalue Add result to accumulator Endif Set output image pixel to accumulator
Convolutie kan worden berekend met behulp van meerdere for-lussen. Maar het gebruik van for-lussen veroorzaakt veel herhaalde berekeningen en ook de grootte van de afbeelding en de kernel neemt toe. Met behulp van de Discrete Fourier Transform-techniek kan het berekenen van convolutie snel worden uitgevoerd. Bij deze techniek wordt de gehele convolutiebewerking omgezet in een eenvoudige vermenigvuldiging.
Bij convolutie treedt het probleem op wanneer de kernel zich dichtbij de rand of hoeken bevindt, omdat de kernel tweedimensionaal is.
Om deze problemen te overwinnen, kunnen de volgende dingen worden gedaan:
- Enen kunnen worden genegeerd
- Er kunnen extra pixels worden gecreëerd nabij de randen.
Extra pixels kunnen op de volgende manieren worden aangemaakt:
- Dubbele randpixel.
- Reflecteer randen
- Pixels kunnen vanaf het andere uiteinde worden gekopieerd.
