Kaartwaarschijnlijkheid is de waarschijnlijkheid van de gebeurtenissen waarbij een pak speelkaarten betrokken is. Zoals we weten is waarschijnlijkheid een van de belangrijke onderwerpen van de wiskunde die zich bezighoudt met de berekening van de mogelijkheid van welke gebeurtenis dan ook. In eenvoudige bewoordingen is de kaartwaarschijnlijkheid een deel van de waarschijnlijkheid waarin we de waarschijnlijkheid vinden dat we een kaart uit het kaartspel trekken. In dit artikel leren we over kaartwaarschijnlijkheid met alle details over de kaartwaarschijnlijkheidsgrafiek, speelkaartwaarschijnlijkheid, hoe je de kaartwaarschijnlijkheid kunt vinden en opgeloste voorbeelden van kaartwaarschijnlijkheid. Laten we beginnen met leren over het onderwerp Kaartwaarschijnlijkheid.
Wat is waarschijnlijkheid?
Waarschijnlijkheid is de tak van de wiskunde die de mogelijkheden bestudeert van welke gebeurtenis dan ook die wel of niet plaatsvindt. Wiskundig gezien is dit niets anders dan de verhouding tussen het aantal gunstige uitkomsten en het totale aantal uitkomsten (steekproefruimte) voor een gebeurtenis.
Enkele voorbeelden uit de praktijk van waarschijnlijkheid zijn:
- Kaartspellen spelen, om de waarschijnlijkheid van het winnen of verliezen van het spel te bepalen.
- Weersvoorspelling, om de regen te voorspellen.
- Verkiezingsresultaten, om te bepalen of de kandidaat zal winnen of verliezen.
- Examenresultaten, om te bepalen of de kandidaat zal slagen of niet zal slagen.
Waarschijnlijkheidsformule
Als E een gebeurtenis is met steekproefruimte S en het aantal gunstige uitkomsten n(E) is, dan wordt de waarschijnlijkheid van gebeurtenis E, d.w.z. P(E), gegeven door:
P(E) = n(E) / n(S)
Wat is kaartwaarschijnlijkheid?
De waarschijnlijkheid dat je een kaart of een verzameling kaarten uit een kaartspel trekt, wordt Kaartwaarschijnlijkheid genoemd. In eenvoudige bewoordingen wordt de waarschijnlijkheid gerelateerd aan speelkaarten kaartwaarschijnlijkheid genoemd. Omdat dit het soort waarschijnlijkheid is, ligt deze altijd tussen 0 en 1. Als we bijvoorbeeld de waarschijnlijkheid moeten vinden dat we een aas uit het kaartspel trekken, d.w.z. 4/52 = 1/13 [Aangezien er 4 azen zijn in het kaartspel van 52 kaarten].
Kaartspel in waarschijnlijkheid
Deck of Cards is een verzameling van 52 kaarten die al duizenden jaren lijken te bestaan. Er wordt aangenomen dat een kaartspel of speelkaarten afkomstig zijn uit India of China. Het eerste gedocumenteerde bewijs van deze kaarten is gevonden in 9e-eeuws China tijdens de Tang-dynastie. Deze kaarten waren vergelijkbaar met de moderne kaarten en ook verdeeld in vier kleuren, maar de naam en het symbool van die kleuren zijn anders, dat wil zeggen munten, reeksen munten, ontelbare en ontelbare tientallen.
Tegenwoordig zijn deze kaarten verkrijgbaar in verschillende ontwerpen en zijn ze onderverdeeld in vier kleuren, namelijk schoppen (♠), klaveren (♣), hart (❤) en ruiten (◆). Voor een enkele gekozen kaart is de monsterruimte 52, dat wil zeggen dat het totale aantal uitkomsten voor een enkele gekozen kaart uit een kaartspel 52 is.
n(S) voor kaartspel = 52
Soorten kaarten in een kaartspel
Elk kaartspel kan op veel manieren worden geclassificeerd. Enkele parameters waarop kaarten kunnen worden geclassificeerd zijn:
- Gebaseerd op kleuren
- Gebaseerd op pakken
Laten we deze classificatie als volgt in detail begrijpen:
Gebaseerd op kleuren
Op basis van kleuren kan een kaartspel in twee categorieën worden ingedeeld:
- Rode kaarten
- Zwarte kaarten
In totaal zijn 52 kaarten gelijkelijk verdeeld in rode en zwarte kaarten, wat betekent dat er 26 rode kaarten en 26 zwarte kaarten in het kaartspel zitten.
Gebaseerd op pakken
Er zijn vier kleuren in het kaartspel:
- Hartjes (❤)
- Diamanten (◆)
- Klavers (♣)
- Schoppen (♠)
Naast deze is er nog een classificatie van kaarten, gebaseerd op de rangorde van de kaarten:
- Ace
- Nummerkaarten
- Gezichtskaarten
Ace
Aas is zo'n kaart die op basis van het spel de belangrijkste of minst belangrijke is. Op deze kaart staat A geschreven en elke reeks heeft één van deze kaarten, d.w.z. vier aaskaarten.
Nummerkaarten
Van 2 tot 10 zijn er 9 kaarten per reeks, dus er zijn in totaal 36 van dergelijke kaarten.
Gezichtskaarten
Gezichtskaarten bevatten, zoals de naam al doet vermoeden, een figuur of gezicht van de figuur op de kaart. Er zijn drie kaarten van elke reeks, d.w.z. boer, vrouw en heer. Er zijn dus in totaal 12 plaatjeskaarten.
Al deze classificaties zijn te zien in de volgende tabel.
Java-erfenis
| Kaartspel (52 kaarten) | ||||
|---|---|---|---|---|
| Gekleurde kaarten | Zwarte kaarten (26 kaarten) | Rode kaarten (26 kaarten) | ||
| Pakken | Schoppen (13 kaarten) | Club (13 kaarten) | Hart (13 kaarten) | Diamant (13 kaarten) |
| Gezichtskaarten (12 kaarten in een kaartspel en 3 kaarten in elke reeks) | K (Koning) | K (Koning) | K (koning) | K (Koning) |
| Q (Koningin) | Q (Koningin) | Q (Koningin) | Q (Koningin) | |
| J (Jack) | J (Jack) | J (Jack) | J (Jack) | |
| Nummerkaarten (36 kaarten in een kaartspel en 9 kaarten in een reeks) | 10 | 10 | 10 | 10 |
| 9 | 9 | 9 | 9 | |
| 8 | 8 | 8 | 8 | |
| 7 | 7 | 7 | 7 | |
| 6 | 6 | 6 | 6 | |
| 5 | 5 | 5 | 5 | |
| 4 | 4 | 4 | 4 | |
| 3 | 3 | 3 | 3 | |
| 2 | 2 | 2 | 2 | |
| Ace-kaarten (4 kaarten in kaartspel en 1 kaart in een reeks) | A (aas) | A (aas) | A (aas) | A (aas) |
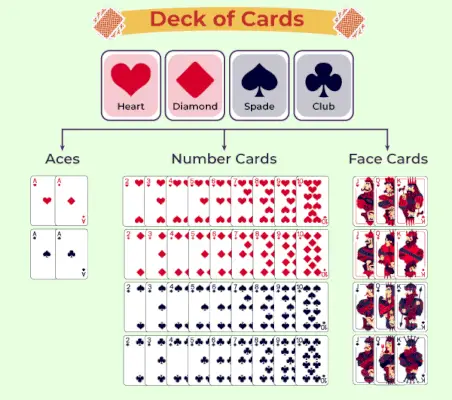
Dek van kaarten grafiek
Het volgende schema geeft de classificatie van het pak speelkaarten weer:
Speelkaartwaarschijnlijkheid
Enkele veel voorkomende gebeurtenissen in kaartkansen worden in de volgende tabel besproken:
| Gebeurtenis E voor het trekken van een kaart | Waarschijnlijkheid P(E) |
|---|---|
| Een Aas | P(E) = 4 / 52 = 1 / 13 |
| Een koning Java return-opdracht | P(E) = 4 / 52 = 1 / 13 |
| Een nummerkaart | P(E) = 36 / 52 = 9 / 13 |
| Een gezichtskaart | P(E) = 12 / 52 = 3 / 13 |
| Een schoppenkaart | P(E) = 13 / 52 = 1 / 4 |
| Een rode kaart | P(E) = 26 / 52 = 1 / 2 |
Hoe de waarschijnlijkheid van kaarten te vinden?
De stappen om de waarschijnlijkheid te bepalen van gebeurtenissen waarbij kaarten betrokken zijn, zijn hetzelfde als alle andere kansen, die als volgt worden gegeven:
Stap 1: Zoek eerst het aantal gunstige uitkomsten van de gegeven vraag.
Stap 2: Zoek vervolgens het totale aantal uitkomsten.
Stap 3: Pas de waarschijnlijkheidsformule toe om de kaartwaarschijnlijkheid te vinden.
Voorbeeld: Wat is de kans dat je een aas trekt uit een pak kaarten?
Antwoord:
Hier is E het geval waarbij een aaskaart wordt getrokken
Totaal aantal uitkomsten in een kaartspel n(S) = 52
Aantal gunstige uitkomsten = n(E) = een aaskaart trekken uit een stapel = 4 (er zijn 4 aaskaarten in 1 stapel)
P(E) = n(E) / n(S) = 4 / 52
P(E) = 1/13
Kans op het trekken van een aaskaart = 1/13
Voorbeeldvragen over kaartwaarschijnlijkheid
Probleem 1: Wat is de kans dat je de volgende kaarten uit een pak kaarten trekt?
(i) een schop
(ii) een zwarte kaart
(iii) een nummerkaart
Oplossing:
(i) Hier is E het geval waarbij een schoppenkaart wordt getrokken
Totaal aantal uitkomsten in een kaartspel n(S) = 52
Aantal gunstige uitkomsten = n(E) = een schoppenkaart trekken uit een stapel = 13 (er zijn 13 kaarten van elke reeks in 1 stapel)
P(E) = n(E) / n(S) = 13 / 52
P(E) = 1 / 4
Kans op het trekken van een schoppen = 1/4
(ii) Hier is E het geval waarbij een zwarte kaart wordt getrokken
Totaal aantal uitkomsten in een kaartspel n(S) = 52
Aantal gunstige uitkomsten = n(E) = zwarte kaart trekken uit stapel = 26 (er zitten 26 zwarte kaarten in 1 stapel)
P(E) = n(E) / n(S) = 26 / 52
P(E) = 1 / 2
Kans op het trekken van een zwarte kaart = 1/2
(iii) Hier is E de gebeurtenis waarbij een nummerkaart wordt getrokken
Totaal aantal uitkomsten in een kaartspel n(S) = 52
Aantal gunstige uitkomsten = n(E) = een nummerkaart trekken uit een stapel = 36 (er zijn 36 nummerkaarten in 1 stapel)
mooiste glimlach ter wereldP(E) = n(E) / n(S) = 36 / 52
P(E) = 9 / 13
Kans op het trekken van een getallenkaart = 9/13
Probleem 2: Wat is de kans dat je de volgende kaarten uit een pak kaarten trekt?
(i) Een koning of een zwarte kaart
(ii) Een rode en aaskaart
Oplossing:
(i) Hier is E de gebeurtenis waarbij een koning of een zwarte kaart wordt getrokken
Totaal aantal uitkomsten in een kaartspel n(S) = 52
Aantal gunstige uitkomsten = n(E) = een koning of een zwarte kaart trekken uit een stapel = 26 + 2 = 28 (er zijn 26 zwarte kaarten waarvan 2 koning zijn en de resterende 2 zwarte koningen in 1 stapel)
P(E) = n(E) / n(S) = 28 / 52
P(E) = 7 / 13
Kans op het trekken van een koning of een zwarte kaart = 7/13
(ii) Hier is E het geval waarbij een rode en een aaskaart wordt getrokken
Totaal aantal uitkomsten in een kaartspel n(S) = 52
Aantal gunstige uitkomsten = n(E) = een rode en aaskaart trekken uit de stapel = 2 (er zijn 26 rode kaarten waarvan 2 aaskaarten)
Volgens de getrokken vraag moet de kaart zowel rood als aas zijn. Daarom is n(E) = 2
P(E) = n(E) / n(S) = 2 / 52
P(E) = 1 / 26
Kans op het trekken van een rode en aaskaart= 1/26
Probleem 3: Wat is de kans dat je de volgende kaarten uit een kaartspel trekt?
(i) Een niet-clubkaart
(ii) Een niet-gezichtskaart
Oplossing:
(i) Hier is E het geval waarbij een niet-clubkaart wordt getrokken
Totaal aantal uitkomsten in een kaartspel n(S) = 52
Aantal gunstige uitkomsten = n(E) = trekken van een niet-clubkaart uit stapel = 39 (Er zijn 13 klaveren in 1 stapel, niet-clubkaart = 52 – 13 = 39)
P(E) = n(E) / n(S) = 39 / 52
P(E) = 3 / 4
Kans op het trekken van een niet-clubkaart = 3 / 4
(ii) Hier is E de gebeurtenis waarbij een niet-plaatjeskaart wordt getrokken
Totaal aantal uitkomsten in een kaartspel n(S) = 52
Aantal gunstige uitkomsten = n(E) = trekken van een niet-beeldkaart uit stapel = 40 (er zijn 12 plaatjeskaarten in 1 stapel, niet-kaartspel = 52 – 12 = 40)
git-statusP(E) = n(E) / n(S) = 40 / 52
P(E) = 10 / 13
Kans op het trekken van een niet-clubkaart = 10 / 13
Probleem 4: Wat is de kans dat je een kaart trekt die noch rood is, noch een plaatjeskaart?
Oplossing:
Hier is E het geval waarbij er geen rode kaart of een plaatjeskaart wordt getrokken
Totaal aantal uitkomsten in een kaartspel n(S) = 52
Aantal gunstige uitkomsten = n(E) = geen rode kaart of plaatjeskaart van de stapel trekken.
Totaal rode kaarten = 26
Er zitten in totaal 12 plaatjeskaarten in een kaartspel, maar er zijn al 6 rode plaatjeskaarten verwijderd. Dus resterende plaatjeskaarten = 12 – 6 = 6
n(E) = 26 + 6 = 32
P(E) = n(E) / n(S) = 32/ 52
P(E) = 8 / 13
Kans op het trekken van een noch rode, noch een plaatjeskaart= 8/13
Probleem 5: Wat is de kans dat je twee kaarten trekt uit een stapel kaarten met vervanging als de eerste kaart een hart is en de tweede kaart een ruiten?
Oplossing:
Kans op het trekken van de eerste kaart als hart = 13 / 52
Na het trekken van de eerste kaart wordt de kaart verwijderd.
Kans op het trekken van de tweede kaart als ruiten = 13/51
runa's in powershellKans op het trekken van de eerste kaart als hart en de tweede als ruiten = (13 / 52) × (13 / 51)
Kans op het trekken van de eerste kaart als hart en de tweede als ruiten = 13/204
Veelgestelde vragen over kaartwaarschijnlijkheid
1. Wat is kaartwaarschijnlijkheid?
De kans dat je een kaart uit de stapel kaarten trekt, wordt kaartwaarschijnlijkheid genoemd.
2. Noem de soorten kleuren in een kaartspel.
Er zijn vier soorten kleuren in een kaartspel. Zij zijn:
- Harten
- Diamanten
- Schoppen
- Clubs
3. Wat is de voorbeeldruimte voor een kaartspel als één kaart uit het kaartspel wordt getrokken?
De voorbeeldruimte voor een kaartspel wanneer één kaart wordt getrokken, bevat 52 uitkomsten.
4. Schrijf de formule voor het vinden van waarschijnlijkheid.
De formule voor het vinden van waarschijnlijkheid wordt gegeven door:
Waarschijnlijkheid van de gebeurtenis = Aantal gunstige gebeurtenissen / Totaal aantal uitkomsten
OF
P(E) = n(E) / n(S)
5. Hoeveel gezichtskaarten zitten er in een kaartspel?
Er zijn 12 gezichtskaarten aanwezig in een kaartspel.
