Sinds de uitvinding van computers gebruiken mensen de term ' Gegevens ' om te verwijzen naar computerinformatie, verzonden of opgeslagen. Er bestaan ​​echter ook gegevens in ordertypen. Gegevens kunnen getallen of teksten zijn die op een stuk papier zijn geschreven, in de vorm van bits en bytes die zijn opgeslagen in het geheugen van elektronische apparaten, of feiten die zijn opgeslagen in de geest van een persoon. Toen de wereld begon te moderniseren, werden deze gegevens een belangrijk aspect van ieders dagelijkse leven, en dankzij verschillende implementaties konden ze deze op een andere manier opslaan.

Gegevens is een verzameling feiten en cijfers of een reeks waarden of waarden van een specifiek formaat die verwijzen naar een enkele reeks itemwaarden. De gegevensitems worden vervolgens geclassificeerd in subitems, de groep items die niet bekend staat als de eenvoudige primaire vorm van het item.

Laten we een voorbeeld bekijken waarbij de naam van een werknemer kan worden opgesplitst in drie subitems: Eerste, Middelste en Laatste. Een ID die aan een medewerker is toegewezen, wordt doorgaans echter als één item beschouwd.

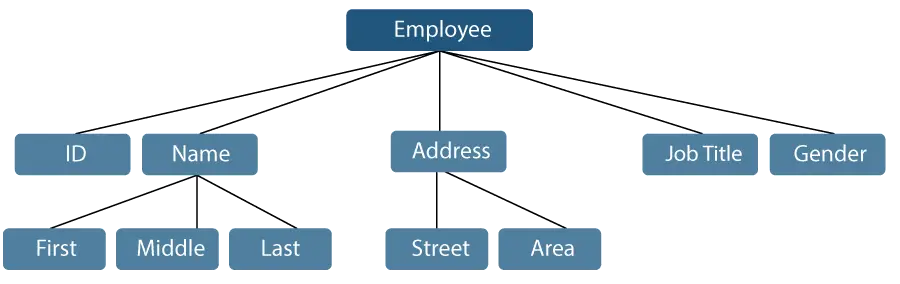
Figuur 1: Weergave van gegevensitems

In het hierboven genoemde voorbeeld zijn de items zoals ID, Leeftijd, Geslacht, Eerste, Midden, Laatste, Straat, Plaats, etc. elementaire gegevensitems. De Naam en het Adres zijn daarentegen groepsgegevensitems.

Wat is datastructuur?

Data structuur is een tak van informatica. De studie van de datastructuur stelt ons in staat de organisatie van gegevens en het beheer van de gegevensstroom te begrijpen om de efficiëntie van elk proces of programma te vergroten. Datastructuur is een bijzondere manier om gegevens in het geheugen van de computer op te slaan en te organiseren, zodat deze gegevens indien nodig in de toekomst gemakkelijk kunnen worden opgehaald en efficiënt kunnen worden gebruikt. De gegevens kunnen op verschillende manieren worden beheerd. Het logische of wiskundige model voor een specifieke organisatie van gegevens staat bekend als een datastructuur.

De reikwijdte van een bepaald datamodel hangt af van twee factoren:

1. Ten eerste moet het voldoende in de structuur worden geladen om de definitieve correlatie van de gegevens met een object uit de echte wereld weer te geven.
2. Ten tweede moet de vorming zo eenvoudig zijn dat men zich kan aanpassen om de gegevens efficiënt te verwerken wanneer dat nodig is.

Enkele voorbeelden van datastructuren zijn arrays, gekoppelde lijsten, stapels, wachtrijen, bomen, enz. Datastructuren worden veel gebruikt in bijna elk aspect van de informatica, dat wil zeggen compilerontwerp, besturingssystemen, grafische afbeeldingen, kunstmatige intelligentie en nog veel meer.

Datastructuren vormen het belangrijkste onderdeel van veel computerwetenschappelijke algoritmen, omdat ze de programmeurs in staat stellen de gegevens op een effectieve manier te beheren. Het speelt een cruciale rol bij het verbeteren van de prestaties van een programma of software, omdat het hoofddoel van de software is om de gegevens van de gebruiker zo snel mogelijk op te slaan en op te halen.

oeps concepten in Java

Basisterminologieën met betrekking tot datastructuren

Datastructuren zijn de bouwstenen van elk software- of programma. Het selecteren van de geschikte datastructuur voor een programma is een uiterst uitdagende taak voor een programmeur.

Hieronder volgen enkele fundamentele terminologieën die worden gebruikt wanneer het om datastructuren gaat:

Gegevens:We kunnen gegevens definiëren als een elementaire waarde of een verzameling waarden. De naam en het ID van de Medewerker zijn bijvoorbeeld de gegevens die betrekking hebben op de Medewerker.Gegevensitems:Een enkele waarde-eenheid staat bekend als Data Item.Groepsartikelen:Gegevensitems met ondergeschikte gegevensitems worden groepsitems genoemd. De naam van een werknemer kan bijvoorbeeld een voor-, middelste en achternaam hebben.Elementaire artikelen:Gegevensitems die niet in subitems kunnen worden verdeeld, worden elementaire items genoemd. Bijvoorbeeld de ID van een Medewerker.Entiteit en attribuut:Een klasse van bepaalde objecten wordt vertegenwoordigd door een Entiteit. Het bestaat uit verschillende attributen. Elk attribuut symboliseert de specifieke eigenschap van die entiteit. Bijvoorbeeld,

Entiteiten met vergelijkbare attributen vormen een Entiteit ingesteld . Elk attribuut van een entiteitsset heeft een bereik van waarden, de set van alle mogelijke waarden die aan het specifieke attribuut kunnen worden toegewezen.

De term 'informatie' wordt soms gebruikt voor gegevens met bepaalde kenmerken van betekenisvolle of verwerkte gegevens.

Veld:Een enkele elementaire informatie-eenheid die het attribuut van een entiteit symboliseert, staat bekend als veld.Dossier:Een verzameling van verschillende gegevensitems staat bekend als een record. Als we het bijvoorbeeld over de werknemersentiteit hebben, kunnen de naam, het ID, het adres en de functietitel ervan worden gegroepeerd om het record voor de werknemer te vormen.Bestand:Een verzameling van verschillende records van één entiteitstype staat bekend als een bestand. Als er bijvoorbeeld 100 werknemers zijn, zijn er 25 records in het gerelateerde bestand met gegevens over elke werknemer.

De noodzaak van datastructuren begrijpen

Omdat applicaties complexer worden en de hoeveelheid gegevens elke dag toeneemt, kan dit leiden tot problemen met het zoeken naar gegevens, de verwerkingssnelheid, de afhandeling van meerdere verzoeken en nog veel meer. Datastructuren ondersteunen verschillende methoden om gegevens efficiënt te organiseren, beheren en opslaan. Met behulp van datastructuren kunnen we de data-items gemakkelijk doorkruisen. Datastructuren zorgen voor efficiëntie, herbruikbaarheid en abstractie.

Waarom moeten we datastructuren leren?

1. Datastructuren en algoritmen zijn twee van de belangrijkste aspecten van informatica.
2. Met datastructuren kunnen we gegevens organiseren en opslaan, terwijl algoritmen ons in staat stellen die gegevens op zinvolle wijze te verwerken.
3. Het leren van datastructuren en algoritmen zal ons helpen betere programmeurs te worden.
4. We zullen code kunnen schrijven die effectiever en betrouwbaarder is.
5. Ook kunnen we problemen sneller en efficiënter oplossen.

De doelstellingen van datastructuren begrijpen

Datastructuren voldoen aan twee complementaire doelstellingen:

Juistheid:Datastructuren zijn ontworpen om correct te werken voor alle soorten invoer op basis van het interessedomein. Met andere woorden: correctheid vormt het primaire doel van de datastructuur, wat altijd afhangt van de problemen die de datastructuur moet oplossen.Efficiëntie:Datastructuren moeten ook efficiënt zijn. Het zou de gegevens snel moeten verwerken zonder veel computerbronnen zoals geheugenruimte te gebruiken. In realtime is de efficiëntie van een datastructuur een sleutelfactor bij het bepalen van het succes en falen van het proces.

Inzicht in enkele belangrijke kenmerken van datastructuren

Enkele van de belangrijkste kenmerken van datastructuren zijn:

Robuustheid:Over het algemeen streven alle computerprogrammeurs ernaar software te produceren die voor elke mogelijke invoer de juiste uitvoer oplevert, samen met een efficiënte uitvoering op alle hardwareplatforms. Dit type robuuste software moet zowel geldige als ongeldige invoer beheren.Aanpassingsvermogen:Het bouwen van softwareapplicaties zoals webbrowsers, tekstverwerkers en internetzoekmachines omvat enorme softwaresystemen die jarenlang correct en efficiënt moeten werken of worden uitgevoerd. Bovendien evolueert software als gevolg van opkomende technologieën of steeds veranderende marktomstandigheden.Herbruikbaarheid:Functies als herbruikbaarheid en aanpassingsvermogen gaan hand in hand. Het is bekend dat de programmeur veel middelen nodig heeft om software te bouwen, waardoor het een kostbare onderneming wordt. Als de software echter op een herbruikbare en aanpasbare manier wordt ontwikkeld, kan deze in de meeste toekomstige toepassingen worden toegepast. Door hoogwaardige datastructuren uit te voeren is het dus mogelijk om herbruikbare software te bouwen, wat kosteneffectief en tijdbesparend lijkt.

Classificatie van datastructuren

Een datastructuur levert een gestructureerde reeks variabelen die op verschillende manieren aan elkaar gerelateerd zijn. Het vormt de basis van een programmeertool die de relatie tussen de data-elementen aangeeft en programmeurs in staat stelt de gegevens efficiënt te verwerken.

We kunnen datastructuren in twee categorieën indelen:

1. Primitieve gegevensstructuur
2. Niet-primitieve gegevensstructuur

De volgende afbeelding toont de verschillende classificaties van gegevensstructuren.

Figuur 2: Classificaties van datastructuren

Primitieve datastructuren

Primitieve datastructurenzijn de datastructuren bestaande uit de cijfers en de tekens die komen ingebouwd in programma's.
1. Deze datastructuren kunnen rechtstreeks worden gemanipuleerd of bediend door instructies op machineniveau.
2. Basisgegevenstypen zoals Geheel getal, zwevend, karakter , En Booleaans vallen onder de Primitieve Datastructuren.
3. Deze gegevenstypen worden ook wel genoemd Eenvoudige gegevenstypen , omdat ze tekens bevatten die niet verder kunnen worden verdeeld

Niet-primitieve gegevensstructuren

Niet-primitieve gegevensstructurenzijn die datastructuren afgeleid van primitieve datastructuren.
1. Deze datastructuren kunnen niet rechtstreeks worden gemanipuleerd of beheerd door instructies op machineniveau.
2. De focus van deze datastructuren ligt op het vormen van een set data-elementen die beide zijn homogeen (hetzelfde gegevenstype) of heterogeen (verschillende gegevenstypen).
3. Op basis van de structuur en rangschikking van gegevens kunnen we deze datastructuren in twee subcategorieën verdelen:
   1. Lineaire gegevensstructuren
   2. Niet-lineaire datastructuren

Lineaire gegevensstructuren

Een datastructuur die een lineaire verbinding tussen de data-elementen behoudt, staat bekend als een lineaire datastructuur. De rangschikking van de gegevens gebeurt lineair, waarbij elk element bestaat uit de opvolgers en voorgangers, behalve het eerste en het laatste gegevenselement. Dit is echter niet noodzakelijkerwijs waar in het geval van geheugen, aangezien de opstelling mogelijk niet opeenvolgend is.

Op basis van geheugentoewijzing worden de lineaire gegevensstructuren verder ingedeeld in twee typen:

Statische datastructuren:De datastructuren met een vaste grootte staan ​​bekend als statische datastructuren. Het geheugen voor deze datastructuren wordt toegewezen op het moment van de compiler, en hun grootte kan na het compileren niet door de gebruiker worden gewijzigd; de daarin opgeslagen gegevens kunnen echter worden gewijzigd.
De Array is het beste voorbeeld van de statische gegevensstructuur, omdat deze een vaste grootte hebben en de gegevens later kunnen worden gewijzigd.Dynamische datastructuren:De datastructuren met een dynamische omvang staan ​​bekend als dynamische datastructuren. Het geheugen van deze datastructuren wordt tijdens de runtime toegewezen en hun grootte varieert tijdens de runtime van de code. Bovendien kan de gebruiker de grootte en de data-elementen die in deze datastructuren zijn opgeslagen tijdens de uitvoering van de code wijzigen.
Gekoppelde lijsten, stapels , En Staarten zijn veelvoorkomende voorbeelden van dynamische datastructuren

Soorten lineaire datastructuren

Hieronder volgt de lijst met lineaire gegevensstructuren die we doorgaans gebruiken:

1. Arrays

Een Array is een gegevensstructuur die wordt gebruikt om meerdere gegevenselementen van hetzelfde gegevenstype in één variabele te verzamelen. In plaats van meerdere waarden van dezelfde gegevenstypen in afzonderlijke namen van variabelen op te slaan, zouden we ze allemaal samen in één variabele kunnen opslaan. Deze verklaring impliceert niet dat we alle waarden van hetzelfde gegevenstype in welk programma dan ook moeten verenigen in één array van dat gegevenstype. Maar er zullen vaak momenten zijn waarop sommige specifieke variabelen van dezelfde gegevenstypen allemaal aan elkaar gerelateerd zijn op een manier die geschikt is voor een array.

Een array is een lijst met elementen waarbij elk element een unieke plaats in de lijst heeft. De data-elementen van de array delen dezelfde variabelenaam; elk heeft echter een ander indexnummer, een subscript genaamd. We hebben toegang tot elk gegevenselement uit de lijst met behulp van de locatie in de lijst. Het belangrijkste kenmerk van de arrays om te begrijpen is dus dat de gegevens worden opgeslagen op aangrenzende geheugenlocaties, waardoor het voor de gebruikers mogelijk wordt gemaakt om door de data-elementen van de array te bladeren met behulp van hun respectieve indexen.

Figuur 3. Een array

bash if-verklaring

Arrays kunnen in verschillende typen worden ingedeeld:

Eendimensionale array:Een array met slechts één rij gegevenselementen staat bekend als een eendimensionale array. Het wordt opgeslagen in een oplopende opslaglocatie.Tweedimensionale array:Een array die uit meerdere rijen en kolommen met gegevenselementen bestaat, wordt een tweedimensionale array genoemd. Het wordt ook wel een matrix genoemd.Multidimensionale array:We kunnen Multidimensional Array definiëren als een array van arrays. Multidimensionale arrays zijn niet gebonden aan twee indices of twee dimensies, omdat ze zoveel indices kunnen bevatten als nodig is.

Enkele toepassingen van Array:

1. We kunnen een lijst met gegevenselementen opslaan die tot hetzelfde gegevenstype behoren.
2. Array fungeert als extra opslag voor andere datastructuren.
3. De array helpt ook bij het opslaan van gegevenselementen van een binaire boom met een vast aantal.
4. Array fungeert ook als opslag van matrices.

2. Gekoppelde lijsten

A Gekoppelde lijst is een ander voorbeeld van een lineaire datastructuur die wordt gebruikt om een ​​verzameling data-elementen dynamisch op te slaan. Gegevenselementen in deze gegevensstructuur worden weergegeven door de knooppunten, verbonden door middel van koppelingen of verwijzingen. Elk knooppunt bevat twee velden, het informatieveld bestaat uit de feitelijke gegevens en het aanwijzerveld bestaat uit het adres van de volgende knooppunten in de lijst. De aanwijzer van het laatste knooppunt van de gekoppelde lijst bestaat uit een nulaanwijzer, aangezien deze naar niets verwijst. In tegenstelling tot de arrays kan de gebruiker de grootte van een gekoppelde lijst dynamisch aanpassen aan de vereisten.

Figuur 4. Een gekoppelde lijst

Gekoppelde lijsten kunnen in verschillende typen worden ingedeeld:

Afzonderlijk gekoppelde lijst:Een enkelvoudig gekoppelde lijst is het meest voorkomende type gekoppelde lijst. Elk knooppunt heeft gegevens en een verwijzingsveld met een adres naar het volgende knooppunt.Dubbel gekoppelde lijst:Een dubbel gekoppelde lijst bestaat uit een informatieveld en twee aanwijzervelden. Het informatieveld bevat de gegevens. Het eerste pointerveld bevat een adres van het vorige knooppunt, terwijl een ander pointerveld een verwijzing naar het volgende knooppunt bevat. We kunnen dus beide kanten op gaan (zowel achteruit als vooruit).Circulair gekoppelde lijst:De Circular Linked List is vergelijkbaar met de Singly Linked List. Het enige belangrijke verschil is dat het laatste knooppunt het adres van het eerste knooppunt bevat en een cirkelvormige lus vormt in de Circular Linked List.

Enkele toepassingen van gekoppelde lijsten:

1. De gekoppelde lijsten helpen ons stapels, wachtrijen, binaire bomen en grafieken van vooraf gedefinieerde grootte te implementeren.
2. We kunnen ook de functie van het besturingssysteem implementeren voor dynamisch geheugenbeheer.
3. Gekoppelde lijsten maken ook polynoomimplementatie voor wiskundige bewerkingen mogelijk.
4. We kunnen Circular Linked List gebruiken om besturingssystemen of applicatiefuncties te implementeren die Round Robin-taken uitvoeren.
5. Circular Linked List is ook handig in een diavoorstelling waarbij een gebruiker terug moet gaan naar de eerste dia nadat de laatste dia is gepresenteerd.
6. Dubbel gelinkte lijst wordt gebruikt om vooruit- en achteruitknoppen in een browser te implementeren om vooruit en achteruit te gaan op de geopende pagina's van een website.

3. Stapels

A Stapel is een lineaire gegevensstructuur die volgt op de LIFO (Last In, First Out)-principe dat bewerkingen mogelijk maakt zoals invoegen en verwijderen vanaf het ene uiteinde van de stapel, d.w.z. Top. Stapels kunnen worden geïmplementeerd met behulp van aaneengesloten geheugen, een array, en niet-aangrenzend geheugen, een gekoppelde lijst. Voorbeelden uit de praktijk van stapels zijn stapels boeken, een pak kaarten, stapels geld en nog veel meer.

Figuur 5. Een realistisch voorbeeld van Stack

De bovenstaande afbeelding vertegenwoordigt het praktijkvoorbeeld van een stapel waarbij de bewerkingen slechts vanaf één kant worden uitgevoerd, zoals het inbrengen en verwijderen van nieuwe boeken vanaf de bovenkant van de stapel. Het houdt in dat het invoegen en verwijderen in de stapel alleen vanaf de bovenkant van de stapel kan worden gedaan. We hebben op elk moment alleen toegang tot de toppen van de Stack.

De primaire bewerkingen in de Stack zijn als volgt:

Duw:De bewerking om een ​​nieuw element in de stapel in te voegen, wordt Push-bewerking genoemd.Knal:De bewerking om elementen uit de stapel te verwijderen of te verwijderen wordt Pop-bewerking genoemd.

Figuur 6. Een stapel

mysql invoegen

Enkele toepassingen van stapels:

1. De Stack wordt gebruikt als tijdelijke opslagstructuur voor recursieve bewerkingen.
2. Stack wordt ook gebruikt als hulpopslagstructuur voor functieaanroepen, geneste bewerkingen en uitgestelde/uitgestelde functies.
3. We kunnen functieaanroepen beheren met behulp van Stacks.
4. Stapels worden ook gebruikt om de rekenkundige uitdrukkingen in verschillende programmeertalen te evalueren.
5. Stapels zijn ook nuttig bij het converteren van infix-expressies naar postfix-expressies.
6. Met stapels kunnen we de syntaxis van de expressie in de programmeeromgeving controleren.
7. We kunnen haakjes matchen met behulp van Stacks.
8. Stapels kunnen worden gebruikt om een ​​string om te keren.
9. Stapels zijn nuttig bij het oplossen van problemen op basis van backtracking.
10. We kunnen Stacks gebruiken voor diepgaand zoeken bij het doorkruisen van grafieken en bomen.
11. Stapels worden ook gebruikt in besturingssysteemfuncties.
12. Stapels worden ook gebruikt in de functies UNDO en REDO tijdens een bewerking.

4. Staarten

A Wachtrij is een lineaire datastructuur vergelijkbaar met een stapel met enkele beperkingen voor het invoegen en verwijderen van de elementen. Het invoegen van een element in een wachtrij gebeurt aan het ene uiteinde, en het verwijderen gebeurt aan een ander of tegenovergesteld uiteinde. We kunnen dus concluderen dat de wachtrijgegevensstructuur het FIFO-principe (First In, First Out) volgt om de gegevenselementen te manipuleren. Implementatie van wachtrijen kan worden gedaan met behulp van arrays, gekoppelde lijsten of stapels. Enkele praktijkvoorbeelden van wachtrijen zijn een rij bij de kassa, een roltrap, een autowasstraat en nog veel meer.

Figuur 7. Een realistisch voorbeeld van wachtrij

De bovenstaande afbeelding is een levensechte illustratie van een bioscoopkaartjesbalie die ons kan helpen de wachtrij te begrijpen, waarbij de klant die als eerste komt altijd als eerste wordt bediend. De klant die als laatste arriveert, wordt ongetwijfeld als laatste bediend. Beide uiteinden van de wachtrij zijn open en kunnen verschillende bewerkingen uitvoeren. Een ander voorbeeld is een foodcourt-lijn waarbij de klant vanaf de achterkant wordt ingebracht, terwijl de klant aan de voorkant wordt verwijderd nadat hij de service heeft verleend waar hij om vroeg.

Hieronder volgen de primaire bewerkingen van de wachtrij:

In wachtrij:Het invoegen of toevoegen van bepaalde gegevenselementen aan de wachtrij wordt Enqueue genoemd. Het inbrengen van elementen gebeurt altijd met behulp van de achterste aanwijzer.Uit wachtrij:Het verwijderen of verwijderen van gegevenselementen uit de wachtrij wordt Dequeue genoemd. Het verwijderen van het element gebeurt altijd met behulp van de vooraanwijzer.

Figuur 8. Wachtrij

Enkele toepassingen van wachtrijen:

1. Wachtrijen worden over het algemeen gebruikt bij de breedtezoekbewerking in Grafieken.
2. Wachtrijen worden ook gebruikt bij de taakplannerbewerkingen van besturingssystemen, zoals een toetsenbordbufferwachtrij om de door gebruikers ingedrukte toetsen op te slaan en een afdrukbufferwachtrij om de door de printer afgedrukte documenten op te slaan.
3. Wachtrijen zijn verantwoordelijk voor CPU-planning, taakplanning en schijfplanning.
4. Prioriteitswachtrijen worden gebruikt bij het downloaden van bestanden in een browser.
5. Wachtrijen worden ook gebruikt om gegevens over te dragen tussen randapparaten en de CPU.
6. Wachtrijen zijn ook verantwoordelijk voor het afhandelen van interrupts die door de gebruikersapplicaties voor de CPU worden gegenereerd.

Niet-lineaire datastructuren

Niet-lineaire datastructuren zijn datastructuren waarbij de data-elementen niet in opeenvolgende volgorde zijn gerangschikt. Hier is het invoegen en verwijderen van gegevens niet lineair mogelijk. Er bestaat een hiërarchische relatie tussen de afzonderlijke gegevensitems.

Soorten niet-lineaire datastructuren

Hieronder volgt de lijst met niet-lineaire gegevensstructuren die we doorgaans gebruiken:

1. Bomen

Een boom is een niet-lineaire gegevensstructuur en een hiërarchie die een verzameling knooppunten bevat, zodat elk knooppunt van de boom een ​​waarde en een lijst met verwijzingen naar andere knooppunten (de 'kinderen') opslaat.

De Tree-datastructuur is een gespecialiseerde methode om gegevens in de computer te ordenen en te verzamelen, zodat deze effectiever kunnen worden gebruikt. Het bevat een centraal knooppunt, structurele knooppunten en subknooppunten die via randen zijn verbonden. We kunnen ook zeggen dat de boomdatastructuur bestaat uit verbonden wortels, takken en bladeren.

Figuur 9. Een boom

Bomen kunnen in verschillende soorten worden ingedeeld:

Binaire boom:Een boomdatastructuur waarbij elk ouderknooppunt maximaal twee kinderen kan hebben, wordt een binaire boom genoemd.Binaire zoekboom:Een binaire zoekboom is een boomgegevensstructuur waarin we eenvoudig een gesorteerde lijst met getallen kunnen bijhouden.AVL-boom:Een AVL-boom is een zelfbalancerende binaire zoekboom waarbij elk knooppunt extra informatie bijhoudt, bekend als een balansfactor, waarvan de waarde -1, 0 of +1 is.B-boom:Een B-Tree is een speciaal type zelfbalancerende binaire zoekboom waarbij elk knooppunt uit meerdere sleutels bestaat en meer dan twee kinderen kan hebben.

Enkele toepassingen van bomen:

soorten netwerken

1. Bomen implementeren hiërarchische structuren in computersystemen zoals mappen en bestandssystemen.
2. Bomen worden ook gebruikt om de navigatiestructuur van een website te implementeren.
3. We kunnen code zoals de code van Huffman genereren met behulp van Trees.
4. Bomen zijn ook nuttig bij de besluitvorming in gamingtoepassingen.
5. Bomen zijn verantwoordelijk voor het implementeren van prioriteitswachtrijen voor op prioriteit gebaseerde planningsfuncties van het besturingssysteem.
6. Bomen zijn ook verantwoordelijk voor het parseren van uitdrukkingen en instructies in de compilers van verschillende programmeertalen.
7. We kunnen Trees gebruiken om gegevenssleutels op te slaan voor indexering voor Database Management System (DBMS).
8. Met Spanning Trees kunnen we beslissingen in computer- en communicatienetwerken routeren.
9. Bomen worden ook gebruikt in het padvindingsalgoritme dat is geïmplementeerd in toepassingen voor kunstmatige intelligentie (AI), robotica en videogames.

2. Grafieken

Een grafiek is een ander voorbeeld van een niet-lineaire gegevensstructuur die bestaat uit een eindig aantal knooppunten of hoekpunten en de randen die deze verbinden. De grafieken worden gebruikt om problemen van de echte wereld aan te pakken, waarbij het probleemgebied wordt aangeduid als een netwerk, zoals sociale netwerken, circuitnetwerken en telefoonnetwerken. De knooppunten of hoekpunten van een grafiek kunnen bijvoorbeeld een enkele gebruiker in een telefoonnetwerk vertegenwoordigen, terwijl de randen de verbinding daartussen via de telefoon vertegenwoordigen.

De grafiekgegevensstructuur, G, wordt beschouwd als een wiskundige structuur die bestaat uit een reeks hoekpunten, V en een reeks randen, E, zoals hieronder weergegeven:

G = (V, E)

Figuur 10. Een grafiek

De bovenstaande figuur vertegenwoordigt een grafiek met zeven hoekpunten A, B, C, D, E, F, G en tien randen [A, B], [A, C], [B, C], [B, D], [B, E], [C, D], [D, E], [D, F], [E, F] en [E, G].

Afhankelijk van de positie van de hoekpunten en randen kunnen de grafieken in verschillende typen worden ingedeeld:

Nulgrafiek:Een grafiek met een lege reeks randen wordt een nulgrafiek genoemd.Triviale grafiek:Een grafiek met slechts één hoekpunt wordt een triviale grafiek genoemd.Eenvoudige grafiek:Een grafiek zonder zelflussen of meerdere randen staat bekend als een eenvoudige grafiek.Multigrafiek:Er wordt gezegd dat een grafiek Multi is als deze uit meerdere randen bestaat maar geen zelflussen.Pseudografiek:Een grafiek met zelflussen en meerdere randen wordt een pseudografiek genoemd.Niet-gerichte grafiek:Een grafiek die uit niet-gerichte randen bestaat, staat bekend als een niet-gerichte grafiek.Gerichte grafiek:Een grafiek die bestaat uit de gerichte randen tussen de hoekpunten staat bekend als een gerichte grafiek.Verbonden grafiek:Een grafiek met ten minste één enkel pad tussen elk paar hoekpunten wordt een verbonden grafiek genoemd.Niet-verbonden grafiek:Een grafiek waarbij er geen pad bestaat tussen ten minste één paar hoekpunten, wordt een niet-verbonden grafiek genoemd.Regelmatige grafiek:Een grafiek waarbij alle hoekpunten dezelfde graad hebben, wordt een reguliere grafiek genoemd.Volledige grafiek:Een grafiek waarin alle hoekpunten een rand hebben tussen elk paar hoekpunten, staat bekend als een volledige grafiek.Cyclusgrafiek:Er wordt gezegd dat een grafiek een cyclus is als deze ten minste drie hoekpunten en randen heeft die een cyclus vormen.Cyclische grafiek:Er wordt gezegd dat een grafiek cyclisch is als en slechts als er ten minste één cyclus bestaat.Acyclische grafiek:Een grafiek met nul cycli wordt een acyclische grafiek genoemd.Eindige grafiek:Een grafiek met een eindig aantal hoekpunten en randen staat bekend als een eindige grafiek.Oneindige grafiek:Een grafiek met een oneindig aantal hoekpunten en randen staat bekend als een oneindige grafiek.Bipartiete grafiek:Een grafiek waarbij de hoekpunten kunnen worden verdeeld in onafhankelijke sets A en B, en alle hoekpunten van set A alleen met enkele randen mogen worden verbonden met de hoekpunten in set B, wordt een bipartiete grafiek genoemd.Vlakke grafiek:Er wordt gezegd dat een grafiek een Planar is als we deze in een enkel vlak kunnen tekenen met twee randen die elkaar snijden.Euler-grafiek:Er wordt gezegd dat een grafiek Euler is als en slechts als alle hoekpunten even graden zijn.Hamiltoniaanse grafiek:Een verbonden grafiek bestaande uit een Hamiltoniaans circuit staat bekend als een Hamiltoniaanse grafiek.

Enkele toepassingen van grafieken:

ssis

1. Grafieken helpen ons routes en netwerken weer te geven in transport-, reis- en communicatietoepassingen.
2. Grafieken worden gebruikt om routes in GPS weer te geven.
3. Grafieken helpen ons ook de onderlinge verbindingen in sociale netwerken en andere netwerkgebaseerde toepassingen weer te geven.
4. Grafieken worden gebruikt in kaarttoepassingen.
5. Grafieken zijn verantwoordelijk voor de weergave van gebruikersvoorkeuren in e-commercetoepassingen.
6. Grafieken worden ook gebruikt in nutsnetwerken om de problemen voor lokale of gemeentelijke bedrijven te identificeren.
7. Grafieken helpen ook bij het beheren van het gebruik en de beschikbaarheid van bronnen in een organisatie.
8. Grafieken worden ook gebruikt om documentlinkkaarten van de websites te maken om de connectiviteit tussen de pagina's via hyperlinks weer te geven.
9. Grafieken worden ook gebruikt in robotbewegingen en neurale netwerken.

Basisbewerkingen van datastructuren

In de volgende sectie bespreken we de verschillende soorten bewerkingen die we kunnen uitvoeren om gegevens in elke gegevensstructuur te manipuleren:

Traversaal:Het doorlopen van een datastructuur betekent dat elk data-element precies één keer wordt benaderd, zodat het kan worden beheerd. Er is bijvoorbeeld verplaatsing nodig bij het afdrukken van de namen van alle medewerkers op een afdeling.Zoekopdracht:Zoeken is een andere datastructuurbewerking, wat betekent dat de locatie wordt gevonden van een of meer data-elementen die aan bepaalde beperkingen voldoen. Een dergelijk data-element kan al dan niet aanwezig zijn in de gegeven set data-elementen. We kunnen de zoekactie bijvoorbeeld gebruiken om de namen te vinden van alle medewerkers die meer dan 5 jaar ervaring hebben.Plaatsing:Invoegen betekent het invoegen of toevoegen van nieuwe gegevenselementen aan de verzameling. We kunnen de invoegbewerking bijvoorbeeld gebruiken om de gegevens toe te voegen van een nieuwe medewerker die het bedrijf onlangs heeft aangenomen.Verwijdering:Verwijderen betekent het verwijderen of verwijderen van een specifiek data-element uit de gegeven lijst met data-elementen. Met de verwijderoperatie kunnen we bijvoorbeeld de naam verwijderen van een medewerker die de baan heeft verlaten.Sorteren:Sorteren betekent dat de gegevenselementen in oplopende of aflopende volgorde worden gerangschikt, afhankelijk van het type toepassing. We kunnen de sorteerbewerking bijvoorbeeld gebruiken om de namen van werknemers op een afdeling in alfabetische volgorde te rangschikken of een schatting te maken van de drie best presterende medewerkers van de maand door de prestaties van de werknemers in aflopende volgorde te rangschikken en de details van de top drie te extraheren.Samenvoegen:Samenvoegen betekent het combineren van gegevenselementen van twee gesorteerde lijsten om één enkele lijst van gesorteerde gegevenselementen te vormen.Creëren:Create is een bewerking die wordt gebruikt om geheugen te reserveren voor de data-elementen van het programma. We kunnen deze bewerking uitvoeren met behulp van een declaratieverklaring. Het creëren van een datastructuur kan op de volgende manieren plaatsvinden:
1. Compileertijd
2. Looptijd
   Bijvoorbeeld de malloc() functie wordt gebruikt in C Taal om datastructuur te creëren.
Selectie:Selectie betekent het selecteren van bepaalde gegevens uit de beschikbare gegevens. We kunnen bepaalde gegevens selecteren door voorwaarden binnen de lus op te geven.Update:Met de Update-bewerking kunnen we de gegevens in de datastructuur bijwerken of wijzigen. We kunnen ook bepaalde gegevens bijwerken door enkele voorwaarden binnen de lus op te geven, zoals de selectiebewerking.Splitsen:Met de splitsoperatie kunnen we gegevens in verschillende subdelen verdelen, waardoor de totale procesvoltooiingstijd wordt verkort.

Het abstracte gegevenstype begrijpen

Volgens de Nationaal Instituut voor Standaarden en Technologie (NIST) , een datastructuur is een rangschikking van informatie, meestal in het geheugen, voor een betere algoritme-efficiëntie. Gegevensstructuren omvatten gekoppelde lijsten, stapels, wachtrijen, bomen en woordenboeken. Ze kunnen ook een theoretische entiteit zijn, zoals de naam en het adres van een persoon.

Uit de hierboven genoemde definitie kunnen we concluderen dat de bewerkingen in de datastructuur het volgende omvatten:

1. Een hoog abstractieniveau, zoals het toevoegen of verwijderen van een item uit een lijst.
2. Een item in een lijst zoeken en sorteren.
3. Toegang tot het item met de hoogste prioriteit in een lijst.

Wanneer de datastructuur dergelijke bewerkingen uitvoert, staat dit bekend als een Abstract gegevenstype (ADT) .

We kunnen het definiëren als een reeks gegevenselementen samen met de bewerkingen op de gegevens. De term 'abstract' verwijst naar het feit dat de gegevens en de fundamentele bewerkingen die erop zijn gedefinieerd, onafhankelijk van hun implementatie worden bestudeerd. Het omvat wat we met de gegevens kunnen doen, niet hoe we het kunnen doen.

Een ADI-implementatie bevat een opslagstructuur om de data-elementen en algoritmen voor fundamentele werking op te slaan. Alle datastructuren, zoals een array, gekoppelde lijst, wachtrij, stapel, enz., zijn voorbeelden van ADT.

De voordelen van het gebruik van ADT's begrijpen

In de echte wereld evolueren programma's als gevolg van nieuwe beperkingen of vereisten, dus het aanpassen van een programma vereist doorgaans een verandering in een of meerdere datastructuren. Stel dat we bijvoorbeeld een nieuw veld in de record van een werknemer willen invoegen om meer details over elke werknemer bij te houden. In dat geval kunnen we de efficiëntie van het programma verbeteren door een Array te vervangen door een Linked-structuur. In een dergelijke situatie is het herschrijven van elke procedure die gebruikmaakt van de gewijzigde structuur ongeschikt. Een beter alternatief is dus om een ​​datastructuur te scheiden van de implementatie-informatie ervan. Dit is het principe achter het gebruik van Abstract Data Types (ADT).

Enkele toepassingen van datastructuren

Hieronder volgen enkele toepassingen van gegevensstructuren:

1. Datastructuren helpen bij de organisatie van gegevens in het geheugen van een computer.
2. Datastructuren helpen ook bij het representeren van de informatie in databases.
3. Datastructuren maken de implementatie van algoritmen mogelijk om door gegevens te zoeken (bijvoorbeeld een zoekmachine).
4. We kunnen de datastructuren gebruiken om de algoritmen te implementeren om gegevens te manipuleren (bijvoorbeeld tekstverwerkers).
5. We kunnen de algoritmen ook implementeren om gegevens te analyseren met behulp van datastructuren (bijvoorbeeld dataminers).
6. Datastructuren ondersteunen algoritmen om de gegevens te genereren (bijvoorbeeld een generator voor willekeurige getallen).
7. Gegevensstructuren ondersteunen ook algoritmen om de gegevens te comprimeren en decomprimeren (bijvoorbeeld een zip-hulpprogramma).
8. We kunnen datastructuren ook gebruiken om algoritmen te implementeren om de gegevens te coderen en decoderen (bijvoorbeeld een beveiligingssysteem).
9. Met behulp van Data Structures kunnen we software bouwen die bestanden en mappen kan beheren (bijvoorbeeld een bestandsbeheerder).
10. We kunnen ook software ontwikkelen die afbeeldingen kan weergeven met behulp van datastructuren. (Bijvoorbeeld een webbrowser of 3D-renderingsoftware).

Daarnaast zijn er, zoals eerder vermeld, nog vele andere toepassingen van Datastructuren die ons kunnen helpen bij het bouwen van elke gewenste software.