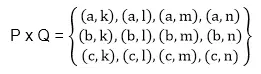Verzamelingen onder de bewerkingen unie, intersectie en complement voldoen aan verschillende wetten (identiteiten) die in Tabel 1 worden vermeld.
Tabel: Wet van de algebra van verzamelingen
| Idempotente wetten | (a) EEN ∪ EEN = A | (b) EEN ∩ EEN = A |
| Associatieve wetten | (a) (A ∪ B) ∪ C = EEN ∪ (B ∪ C) | (b) (A ∩ B) ∩ C = EEN ∩ (B ∩ C) |
| Commutatieve wetten | (a) EEN ∪ B = B ∪ A | (b) EEN ∩ B = B ∩ A |
| Distributieve wetten | (a) EEN ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) | (b) EEN ∩ (B ∪ C) =(A ∩ B) ∪ (A ∩ C) |
| De Morgans wetten | (a) (A ∪B)C=EENC∩ BC | (b) (A ∩B)C=EENC∪ BC |
| Identiteitswetten | (a) EEN ∪ ∅ = A (b) EEN ∪ U = U | (c) EEN ∩ U =A (d) EEN ∩ ∅ = ∅ |
| Complementeer wetten | (a) EEN ∪ AC= U (b) EEN ∩ AC= ∅ | (c) UC= ∅ (d) ∅C= U |
| Involutie wet | (een) (AC)C= EEN |
Tabel 1 toont de wet van de algebra van verzamelingen.
Voorbeeld 1: Bewijs Idempotente wetten:
(a) A ∪ A = A
Oplossing:
Since, B ⊂ A ∪ B, therefore A ⊂ A ∪ A Let x ∈ A ∪ A ⇒ x ∈ A or x ∈ A ⇒ x ∈ A ∴ A ∪ A ⊂ A As A ∪ A ⊂ A and A ⊂ A ∪ A ⇒ A =A ∪ A. Hence Proved.
(b) A ∩ A = A
Oplossing:
Since, A ∩ B ⊂ B, therefore A ∩ A ⊂ A Let x ∈ A ⇒ x ∈ A and x ∈ A ⇒ x ∈ A ∩ A ∴ A ⊂ A ∩ A As A ∩ A ⊂ A and A ⊂ A ∩ A ⇒ A = A ∩ A. Hence Proved.
Voorbeeld 2: Bewijs associatieve wetten:
(a) (A ∪ B) ∪ C = A ∪ (B ∪ C)
Oplossing:
Let some x ∈ (A'∪ B) ∪ C ⇒ (x ∈ A or x ∈ B) or x ∈ C ⇒ x ∈ A or x ∈ B or x ∈ C ⇒ x ∈ A or (x ∈ B or x ∈ C) ⇒ x ∈ A or x ∈ B ∪ C ⇒ x ∈ A ∪ (B ∪ C). Similarly, if some x ∈ A ∪ (B ∪ C), then x ∈ (A ∪ B) ∪ C. Thus, any x ∈ A ∪ (B ∪ C) ⇔ x ∈ (A ∪ B) ∪ C. Hence Proved.
(b) (A ∩ B) ∩ C = A ∩ (B ∩ C)
Oplossing:
Let some x ∈ A ∩ (B ∩ C) ⇒ x ∈ A and x ∈ B ∩ C ⇒ x ∈ A and (x ∈ B and x ∈ C) ⇒ x ∈ A and x ∈ B and x ∈ C ⇒ (x ∈ A and x ∈ B) and x ∈ C) ⇒ x ∈ A ∩ B and x ∈ C ⇒ x ∈ (A ∩ B) ∩ C. Similarly, if some x ∈ A ∩ (B ∩ C), then x ∈ (A ∩ B) ∩ C Thus, any x ∈ (A ∩ B) ∩ C ⇔ x ∈ A ∩ (B ∩ C). Hence Proved.
Voorbeeld 3: Bewijs commutatieve wetten
(a) A ∪ B = B ∪ A
Oplossing:
To Prove A ∪ B = B ∪ A A ∪ B = {x: x ∈ A or x ∈ B} = {x: x ∈ B or x ∈ A} (∵ Order is not preserved in case of sets) A ∪ B = B ∪ A. Hence Proved. (b) A ∩ B = B ∩ A
Oplossing:
To Prove A ∩ B = B ∩ A A ∩ B = {x: x ∈ A and x ∈ B} = {x: x ∈ B and x ∈ A} (∵ Order is not preserved in case of sets) A ∩ B = B ∩ A. Hence Proved. Voorbeeld 4: Bewijs distributieve wetten
(a) A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
Oplossing:
To Prove Let x ∈ A ∪ (B ∩ C) ⇒ x ∈ A or x ∈ B ∩ C ⇒ (x ∈ A or x ∈ A) or (x ∈ B and x ∈ C) ⇒ (x ∈ A or x ∈ B) and (x ∈ A or x ∈ C) ⇒ x ∈ A ∪ B and x ∈ A ∪ C ⇒ x ∈ (A ∪ B) ∩ (A ∪ C) Therefore, A ∪ (B ∩ C) ⊂ (A ∪ B) ∩ (A ∪ C)............(i) Again, Let y ∈ (A ∪ B) ∩ (A ∪ C) ⇒ y ∈ A ∪ B and y ∈ A ∪ C ⇒ (y ∈ A or y ∈ B) and (y ∈ A or y ∈ C) ⇒ (y ∈ A and y ∈ A) or (y ∈ B and y ∈ C) ⇒ y ∈ A or y ∈ B ∩ C ⇒ y ∈ A ∪ (B ∩ C) Therefore, (A ∪ B) ∩ (A ∪ C) ⊂ A ∪ (B ∩ C)............(ii) Combining (i) and (ii), we get A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C). Hence Proved
(b) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
Oplossing:
To Prove Let x ∈ A ∩ (B ∪ C) ⇒ x ∈ A and x ∈ B ∪ C ⇒ (x ∈ A and x ∈ A) and (x ∈ B or x ∈ C) ⇒ (x ∈ A and x ∈ B) or (x ∈ A and x ∈ C) ⇒ x ∈ A ∩ B or x ∈ A ∩ C ⇒ x ∈ (A ∩ B) ∪ (A ∪ C) Therefore, A ∩ (B ∪ C) ⊂ (A ∩ B) ∪ (A ∪ C)............ (i) Again, Let y ∈ (A ∩ B) ∪ (A ∪ C) ⇒ y ∈ A ∩ B or y ∈ A ∩ C ⇒ (y ∈ A and y ∈ B) or (y ∈ A and y ∈ C) ⇒ (y ∈ A or y ∈ A) and (y ∈ B or y ∈ C) ⇒ y ∈ A and y ∈ B ∪ C ⇒ y ∈ A ∩ (B ∪ C) Therefore, (A ∩ B) ∪ (A ∪ C) ⊂ A ∩ (B ∪ C)............ (ii) Combining (i) and (ii), we get A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∪ C). Hence Proved
Voorbeeld 5: Bewijs de wetten van De Morgan
(a) (A ∪B)<sup>c</sup>=A<sup>c</sup>∩ B<sup>c</sup>
Oplossing:
To Prove (A ∪B)<sup>c</sup>=A<sup>c</sup>∩ B<sup>c</sup> Let x ∈ (A ∪B)<sup>c</sup> ⇒ x ∉ A ∪ B (∵ a ∈ A ⇔ a ∉ A<sup>c</sup>) ⇒ x ∉ A and x ∉ B ⇒ x ∉ A<sup>c</sup> and x ∉ B<sup>c</sup> ⇒ x ∉ A<sup>c</sup>∩ B<sup>c</sup> Therefore, (A ∪B)<sup>c</sup> ⊂ A<sup>c</sup>∩ B<sup>c</sup>............. (i) Again, let x ∈ A<sup>c</sup>∩ B<sup>c</sup> ⇒ x ∈ A<sup>c</sup> and x ∈ B<sup>c</sup> ⇒ x ∉ A and x ∉ B ⇒ x ∉ A ∪ B ⇒ x ∈ (A ∪B)<sup>c</sup> Therefore, A<sup>c</sup>∩ B<sup>c</sup> ⊂ (A ∪B)<sup>c</sup>............. (ii) Combining (i) and (ii), we get A<sup>c</sup>∩ B<sup>c</sup> =(A ∪B)<sup>c</sup>. Hence Proved.
(b) (A ∩B)<sup>c</sup> = A<sup>c</sup>∪ B<sup>c</sup>
Oplossing:
Let x ∈ (A ∩B)<sup>c</sup> ⇒ x ∉ A ∩ B (∵ a ∈ A ⇔ a ∉ A<sup>c</sup>) ⇒ x ∉ A or x ∉ B ⇒ x ∈ A<sup>c</sup> and x ∈ B<sup>c</sup> ⇒ x ∈ A<sup>c</sup>∪ B<sup>c</sup> ∴ (A ∩B)<sup>c</sup>⊂ (A ∪B)<sup>c</sup>.................. (i) Again, Let x ∈ A<sup>c</sup>∪ B<sup>c</sup> ⇒ x ∈ A<sup>c</sup> or x ∈ B<sup>c</sup> ⇒ x ∉ A or x ∉ B ⇒ x ∉ A ∩ B ⇒ x ∈ (A ∩B)<sup>c</sup> ∴ A<sup>c</sup>∪ B<sup>c</sup>⊂ (A ∩B)<sup>c</sup>.................... (ii) Combining (i) and (ii), we get(A ∩B)<sup>c</sup>=A<sup>c</sup>∪ B<sup>c</sup>. Hence Proved.
Voorbeeld 6: Bewijs identiteitswetten.
(a) A ∪ ∅ = A
Oplossing:
To Prove A ∪ ∅ = A Let x ∈ A ∪ ∅ ⇒ x ∈ A or x ∈ ∅ ⇒ x ∈ A (∵x ∈ ∅, as ∅ is the null set ) Therefore, x ∈ A ∪ ∅ ⇒ x ∈ A Hence, A ∪ ∅ ⊂ A. We know that A ⊂ A ∪ B for any set B. But for B = ∅, we have A ⊂ A ∪ ∅ From above, A ⊂ A ∪ ∅ , A ∪ ∅ ⊂ A ⇒ A = A ∪ ∅. Hence Proved.
(b) A ∩ ∅ = ∅
Oplossing:
To Prove A ∩ ∅ = ∅ If x ∈ A, then x ∉ ∅ (∵∅ is a null set) Therefore, x ∈ A, x ∉ ∅ ⇒ A ∩ ∅ = ∅. Hence Proved.
(c) A ∪ U = U
Oplossing:
To Prove A ∪ U = U Every set is a subset of a universal set. ∴ A ∪ U ⊆ U Also, U ⊆ A ∪ U Therefore, A ∪ U = U. Hence Proved.
(d) A ∩ U = A
Oplossing:
To Prove A ∩ U = A We know A ∩ U ⊂ A................. (i) So we have to show that A ⊂ A ∩ U Let x ∈ A ⇒ x ∈ A and x ∈ U (∵ A ⊂ U so x ∈ A ⇒ x ∈ U ) ∴ x ∈ A ⇒ x ∈ A ∩ U ∴ A ⊂ A ∩ U................. (ii) From (i) and (ii), we get A ∩ U = A. Hence Proved.
Voorbeeld 7: Bewijs complementwetten
(a) A ∪ A<sup>c</sup>= U
Oplossing:
To Prove A ∪ A<sup>c</sup>= U Every set is a subset of U ∴ A ∪ A<sup>c</sup> ⊂ U.................. (i) We have to show that U ⊆ A ∪ A<sup>c</sup> Let x ∈ U ⇒ x ∈ A or x ∉ A ⇒ x ∈ A or x ∈ A<sup>c</sup> ⇒ x ∈ A ∪ A<sup>c</sup> ∴ U ⊆ A ∪ A<sup>c</sup>................... (ii) From (i) and (ii), we get A ∪ A<sup>c</sup>= U. Hence Proved.
(b) A ∩ A<sup>c</sup>=∅
Oplossing:
As ∅ is the subset of every set ∴ ∅ ⊆ A ∩ A<sup>c</sup>..................... (i) We have to show that A ∩ A<sup>c</sup> ⊆ ∅ Let x ∈ A ∩ A<sup>c</sup> ⇒ x ∈ A and x ∈ A<sup>c</sup> ⇒ x ∈ A and x ∉ A ⇒ x ∈ ∅ ∴ A ∩ A<sup>c</sup> ⊂∅..................... (ii) From (i) and (ii), we get A∩ A<sup>c</sup>=∅. Hence Proved.
(c) U<sup>c</sup>= ∅
Oplossing:
Let x ∈ U<sup>c</sup> ⇔ x ∉ U ⇔ x ∈ ∅ ∴ U<sup>c</sup>= ∅. Hence Proved. (As U is the Universal Set).
(d) ∅<sup>c</sup> = U
Oplossing:
Let x ∈ ∅<sup>c</sup> ⇔ x ∉ ∅ ⇔ x ∈ U (As ∅ is an empty set) ∴ ∅<sup>c</sup> = U. Hence Proved.
Voorbeeld 8: Bewijs de wet van de involutie
(a) (A<sup>c</sup> )<sup>c</sup> A.
Oplossing:
Let x ∈ (A<sup>c</sup> )<sup>c</sup> ⇔ x ∉ A<sup>c</sup>⇔ x ∈ a ∴ (A<sup>c</sup> )<sup>c</sup> =A. Hence Proved.
Dualiteit:
De dubbele E∗ van E is de vergelijking die wordt verkregen door elk voorkomen van ∪, ∩, U en ∅ in E te vervangen door respectievelijk ∩, ∪, ∅ en U. De dubbele van bijvoorbeeld
(U ∩ A) ∪ (B ∩ A) = A is (∅ ∪ A) ∩ (B ∪ A) = A
Als dualiteitsprincipe wordt opgemerkt dat als een vergelijking E een identiteit is, de duale E∗ ook een identiteit is.
Principe van uitbreiding:
Volgens het principe van uitbreiding zijn twee sets, A en B, hetzelfde als en slechts als ze dezelfde leden hebben. Gelijke verzamelingen duiden we aan met A=B.
If A= {1, 3, 5} and B= {3, 1, 5}, then A=B i.e., A and B are equal sets. If A= {1, 4, 7} and B= {5, 4, 8}, then A≠ B i.e.., A and B are unequal sets. Cartesisch product van twee sets:
Het cartesiaanse product van twee verzamelingen P en Q in die volgorde is de verzameling van alle geordende paren waarvan het eerste lid tot de verzameling P behoort en het tweede lid tot de verzameling Q en wordt aangegeven met P x Q, d.w.z.
Java-reeks van array
P x Q = {(x, y): x ∈ P, y ∈ Q}. Voorbeeld: Stel P = {a, b, c} en Q = {k, l, m, n}. Bepaal het cartesiaanse product van P en Q.
Oplossing: Het cartesiaanse product van P en Q is